与函数有关的恒成立问题

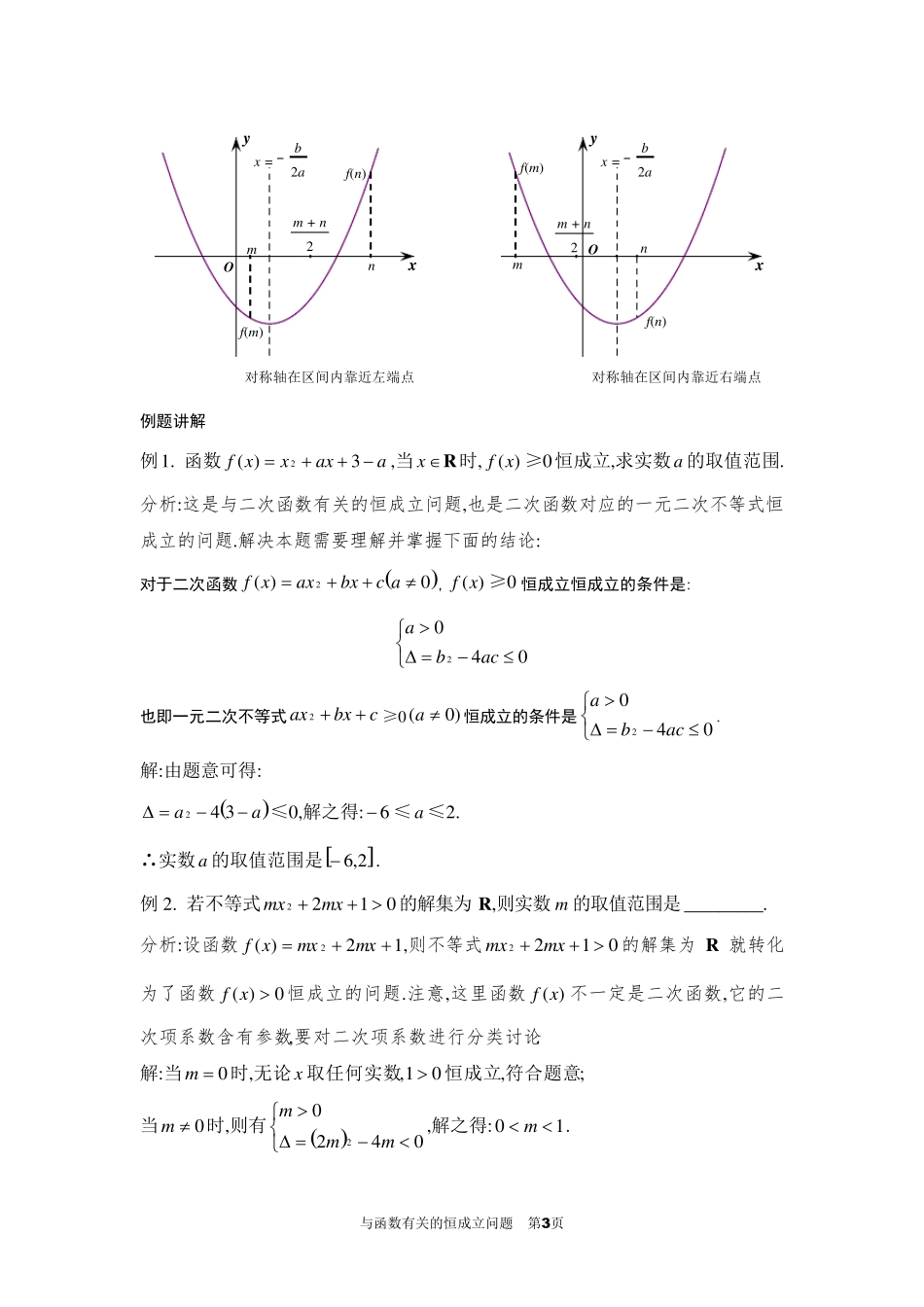
与函数有关的恒成立问题 第1页 与函数有关的恒成立问题 最常见的是二次函数的恒成立问题,分为两种题型: （1）二次函数在R 上的恒成立问题; （2）二次函数在给定区间上的恒成立问题. 对于二次函数)0(2acbxaxy: ①若cbxax2≥0 在R 上恒成立,则00a; ②若cbxax2≤0 在R 上恒成立,则00a. 函数恒成立问题的求解方法（转化化归思想）分离参数法 函数的恒成立问题,一般将其转化为求函数的最大值或最小值问题: ①a ≤)(xf恒成立a≤min)(xf; ②a ≥)(xf恒成立a≥max)(xf. 在求解恒成立问题时,把参数分离出来,使不等式的一端是含有参数的代数式,另一端是一个区间上的具体函数,这样就把问题转化为一端是函数,另一端是参数的不等式,便于问题的解决.这种方法叫做分离参数法. 结论 二次函数的给定闭区间上的最值问题 求二次函数的最大（小）值有两种类型:一是函数的定义域为实数集 R,这时只要根据抛物线的开口方向,应用配方法即可求出最大（小）值;二是函数的定义域为某一区间,这是函数的最值由它的单调性确定,而它的单调性又与抛物线的开口方向和对称轴的位置（在区间上、在区间的左侧、在区间的右侧）来决定,当开口方向或对称轴位置不确定时,还需要进行分类讨论. 求二次函数0)(2acbxaxxf在区间nm,上的最值分为以下三种情况: （1）对称轴在区间的左侧 若mabx2,则)(xf在区间nm,上是增函数,最大值为 nf,最小值为 mf; （2）对称轴在区间内 若m ≤ab2≤ n ,则)(xf的最小值为abacabf4422,最大值为 mf、  nf中的 与函数有关的恒成立问题 第2页 较大者（或区间端点nm,中与直线 abx2的距离较大的那一个端点所对应的函数值）; 即最小值为abacabf4422,最大值为    nfmfxf,maxmax . （3）对称轴在区间的右侧 若nabx2,则)(xf在区间nm,上是减函数,最大值为 mf,最小值为 nf. 注意:当抛物线的对称轴 abx2在区间nm,上,即m ≤ab2≤ n 时,函数的最小值在顶点处获得,为顶点的纵坐标,即abacabfxf442)(2min,函数最大值的确定需要分为两种情况: 区间nm,的中点为2nm （由中点坐标公式得到）. ①当m ≤ab2≤2nm 时（即右端点n 距离对称轴较远）,函数的最大值为 nf; ②当abnm22≤ m 时（即...