传热学上机报告

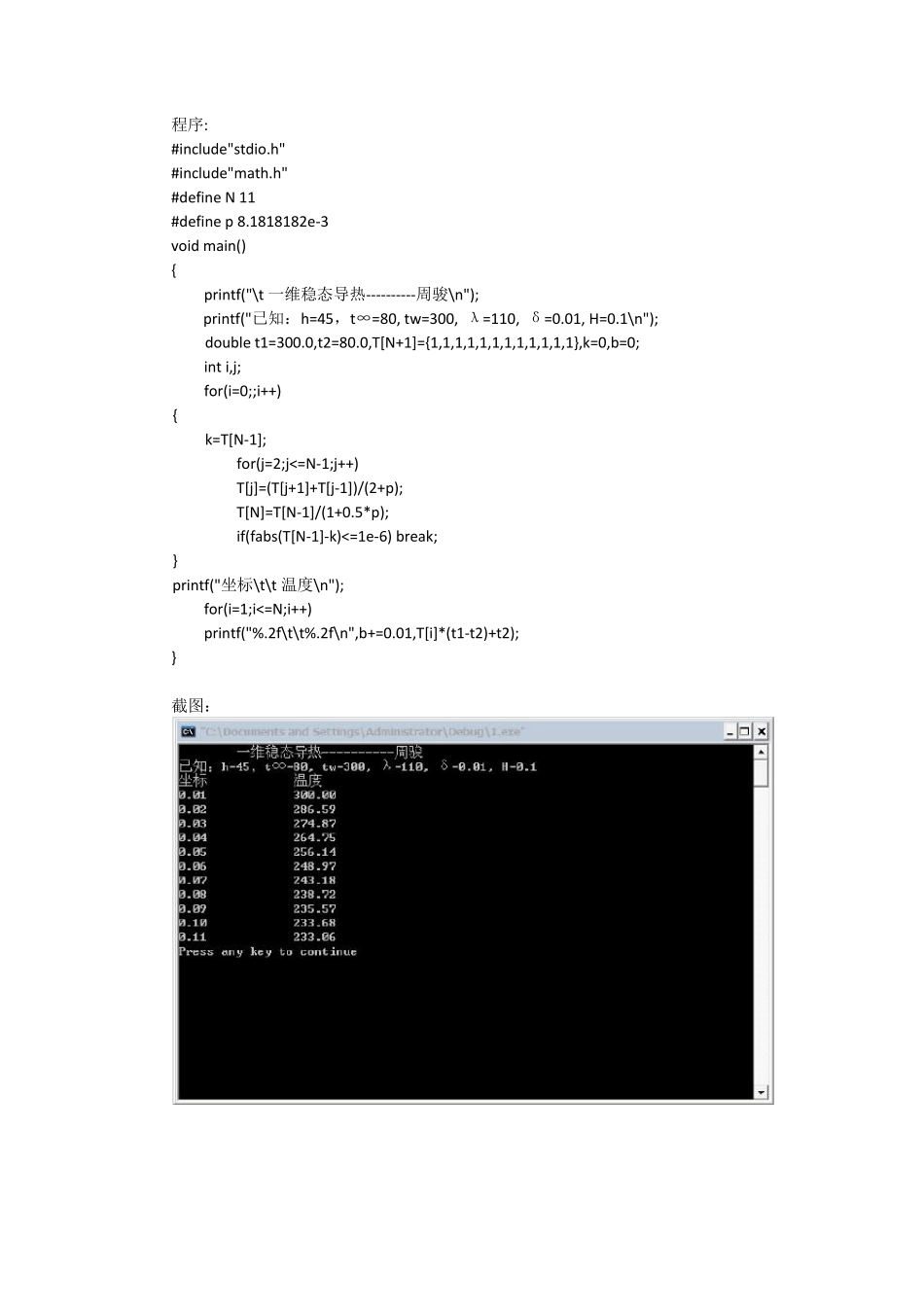
传热学上机报告 学号： 姓名： 一维稳态导热的数值计算 1.1 物理问题 一个等截面直肋，处于温度ᵆ∞=80的流体中。肋表面与流体之间的对流换热系数为h =45W/(ᵅ2 ∙ ℃),肋基处温度tᵆ = 300℃，肋端绝热。肋片由铝合金制成，其导热系数为λ =110W/(m ∙ ℃)，肋片厚度为δ = 0.01m，高度为H=0.1m。试计算肋内的温度分布及肋的总换热量。 1.2 数学描述及其解析解 引入无量纲过余温度θ = ᵆ− ᵆ∞tᵆ− ᵆ∞，则无量纲温度描述的肋片导热微分方程及其边界条件：2220dmdx x=0,θ=θw=1 x=H,0x 其中 Ahpm  λ 上述数学模型的解析解为：[ ()]()()wch m x Httttch mH ()()whp ttth mHm  1.3 数值离散 1.3.1 区域离散 计算区域总节点数取N。 1.3.2 微分方程的离散 对任一借点i 有：2220idmdx  用θ在节点i 的二阶差分代替θ在节点i 的二阶导数，得：211220iiiimx 整理成迭代形式：112212iiimx (i=2,3… … ,N-1) 1.3.3 边界条件离散 补充方程为：11w 右边界为第二类边界条件，边界节点N 的向后差分得：10NNx，将此式整理为迭代形式，得：N1N 1.3.4 最终离散格式 11w 112212iiimx (i=2,3… … ,N-1) N1N 1.3.5 代数方程组的求解及其程序 假定一个温度场的初始发布，给出各节点的温度初值：01 ，02 ，… .，0N 。将这些初值代入离散格式方程组进行迭代计算，直至收敛。假设第 K 步迭代完成，则 K+1 次迭代计算式为：K 11w  11112212iiKKKimx (i=2,3… … ,N-1) 111NKKN 程序: #include"stdio.h" #include"math.h" #define N 11 #define p 8.1818182e-3 void main() { printf("\t 一维稳态导热----------周骏\n"); printf("已知：h=45，t∞=80, tw=300, λ=110, δ=0.01, H=0.1\n"); double t1=300.0,t2=80.0,T[N+1]={1,1,1,1,1,1,1,1,1,1,1,1},k=0,b=0; int i,j; for(i=0;;i++) { k=T[N-1]; for(j=2;j<=N-1;j++) T[j]=(T[j+1]+T[j-1])/(2+p); T[N]=T[N-1]/(1+0.5*p); if(fabs(T[N-1]-k)<=1e-6) break; } printf("坐标\t\t 温度\n"); for(i=1;i<=N;i++) printf("%.2f\t\t%.2f\n",b+=0.01,T[i]*(t1...