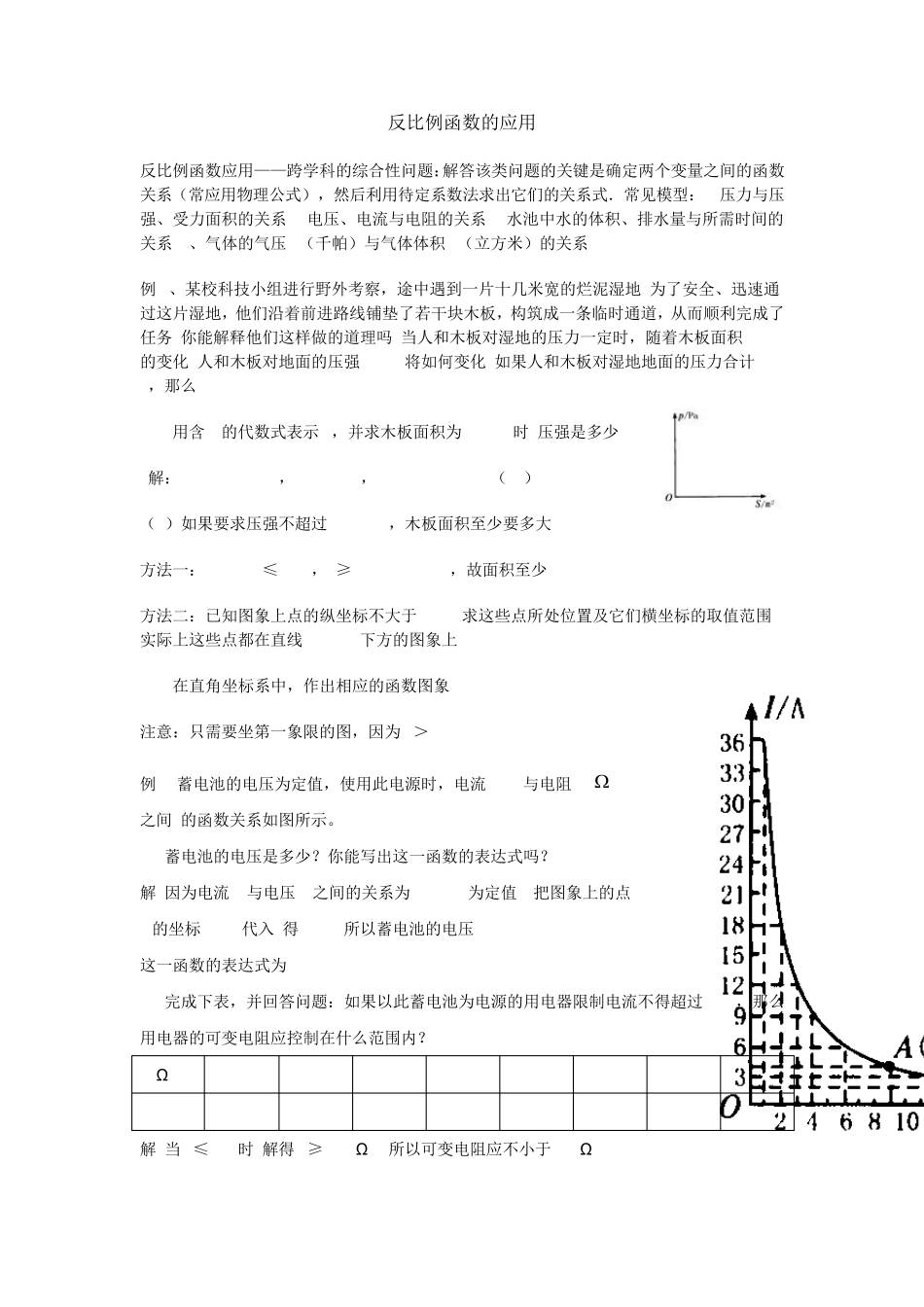
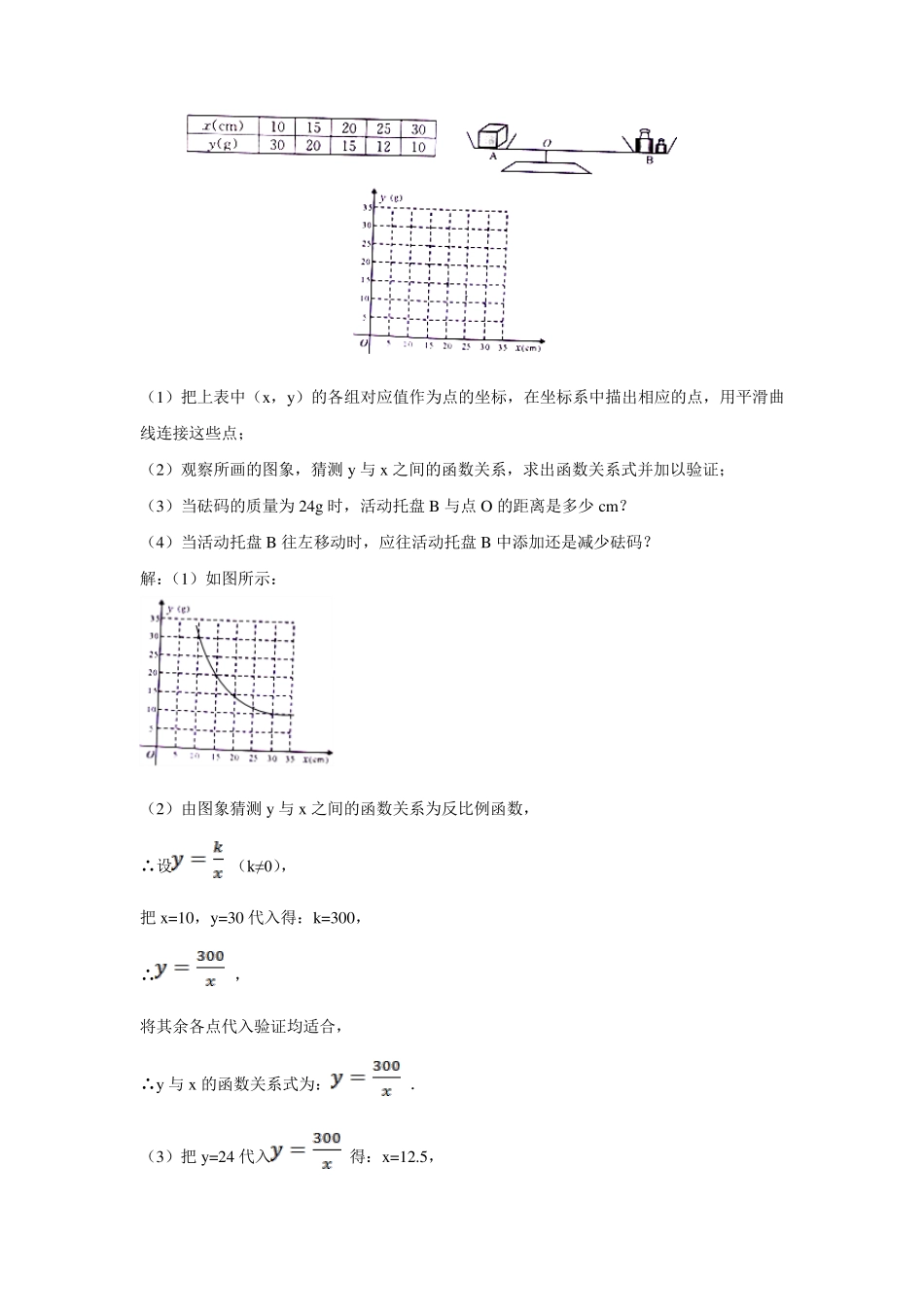
反比例函数的应用 反比例函数应用——跨学科的综合性问题:解答该类问题的关键是确定两个变量之间的函数关系(常应用物理公式),然后利用待定系数法求出它们的关系式.常见模型:1.压力与压强、受力面积的关系 2.电压、电流与电阻的关系 3.水池中水的体积、排水量与所需时间的关系 4、气体的气压 P(千帕)与气体体积 V(立方米)的关系 例1、某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积 S(m2)的变化,人和木板对地面的压强 p(Pa)将如何变化?如果人和木板对湿地地面的压力合计 600 N,那么 (1) 用含 S的代数式表示 p,并求木板面积为 0.2 m2时.压强是多少? 解:P=F/S=600/S ,S=0.2 m2 ,P=600/0.2=1200(Pa) (2)如果要求压强不超过 6000 Pa,木板面积至少要多大? 方法一:P=600/S≤6000,S≥600/6000=0.1,故面积至少 0.1 m2 方法二:已知图象上点的纵坐标不大于 6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线 P=6000下方的图象上 (3) 在直角坐标系中,作出相应的函数图象. 注意:只需要坐第一象限的图,因为 S>0. 例2.蓄电池的电压为定值,使用此电源时,电流 I(A)与电阻 R( )之间 的函数关系如图所示。 (1)蓄电池的电压是多少?你能写出这一函数的表达式吗? 解:因为电流 I与电压 U之间的关系为 IR=U(U为定值),把图象上的点A的坐标(9,4)代入,得 U=36.所以蓄电池的电压 U=36V. 这一函数的表达式为:I=36/R (2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过 10A,那么用电器的可变电阻应控制在什么范围内? R(Ω ) 3 4 5 6 7 8 9 10 I(A) 4 解:当 I≤10A时,解得 R≥3.6(Ω ).所以可变电阻应不小于 3.6Ω . 试一试1.某蓄水池的排水管每时排水8m3 ,6h可将满池水全部排空。 (1)蓄水池的容积是多少? 解:蓄水池的容积为:8×6=48(m3). (2)如果增加排水管,使每时的排水量达到 Q(3m ),那么将满池水排空所需的时间 t(h)将如何变化? 答:此时所需时间 t(h)将减少. (3)写出 t与 Q之间的关系式; 解:t与 Q之间的函数关系式为: (4)如果准备在 5h内将满池水排空,那么每时的排水量至少为多少? 解:当 t=5h时,Q=48...