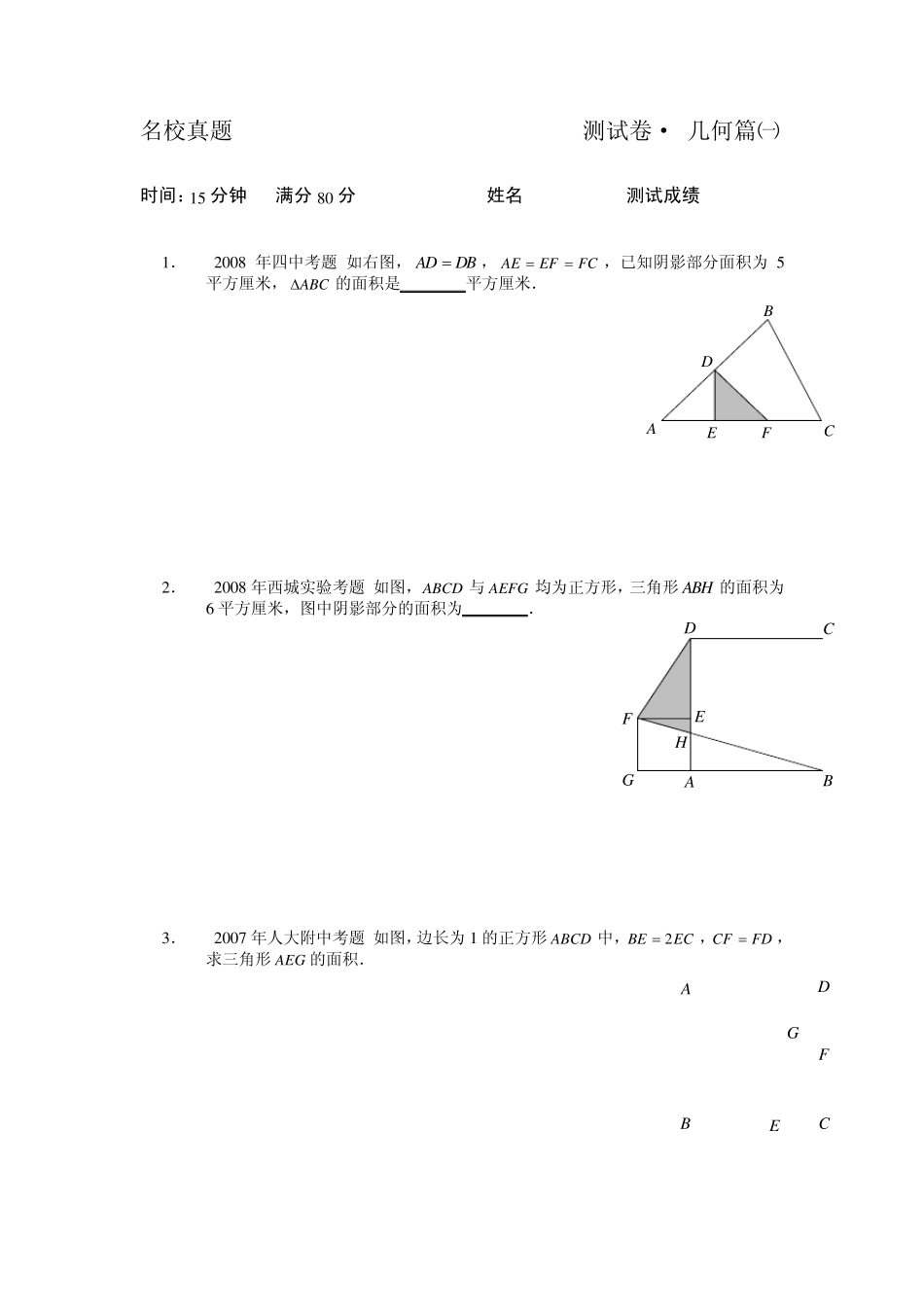
名校真题 gvb 测试卷· 计算计数篇 时间:1 5 分钟 满分 8 0 分 姓名_________ 测试成绩_________ 1 . (2 0 0 8 年 1 0 1 中学考题) 计算: 11111111() 1288244880120168224288 . 2 . (2 0 0 8 年清华附中考题) 1111111111111111())()5791179111357911137911()( . 3 . (2 0 0 8 年清华附中考题)由 0 ,1 ,2 ,3 ,4 ,5 组成的没有重复数字的六位数中,百位不是 2 的奇数有 个. 4 . (2 0 0 8 年实验中学考题)新年联欢会上,共有 9 0 人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少 7 人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多 4 人;5 0 人没有参加演奏;1 0 人同时参加了跳舞和合唱但没有参加演奏;4 0 人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有________人. 名校真题 测试卷·组合原理篇 时间:1 5 分钟 满分 5 分 姓名_________ 测试成绩_________ 1 . (2 0 0 9 年清华附中入学测试题)如图,在时钟的表盘上任意作9 个1 2 0 °的扇形,使得每一个扇形都恰好覆盖 4 个数,且每两个扇形覆盖的数不全相同,求证:一定可以找到 3 个扇形,恰好覆盖整个表盘上的数.并举一个反例说明,作8 个扇形将不能保证上述结论成立. 1 11 09876543211 2 2 . (2 0 0 9年清华附中入学测试题)对四位数 abcd ,若存在质数 p 和正整数 k ,使kabcdp ,且5pa b c dp ,求这样的四位数的最小值,并说明理由. 3 . (2 0 0 8 年西城实验考题)有 5 个连续自然数,它们的和为一个平方数,中间三数的和为立方数,则这五个数中最小数的最小值为 . 4 . (2 0 0 8 年 1 0 1 中学考题)一根 1 0 1 厘米长的木棒,从同一端开始,第一次每隔 2 厘米画一个刻度,第二次每隔 3 厘米画一个刻度,第三次每隔 5 厘米画一个刻度,如果按刻度把木棒截断,那么可以截出 段. 名校真题 测试卷· 几何篇㈠ 时间:15 分钟 满分 80 分 姓名_________ 测试成绩_________ 1. (2008 年四中考题)如右图, ADDB, AEEFFC,已知阴影部分面积为 5平方厘米,ABC的面积是 平方厘米. FEDCBA 2...