周期三角波的傅里叶级数

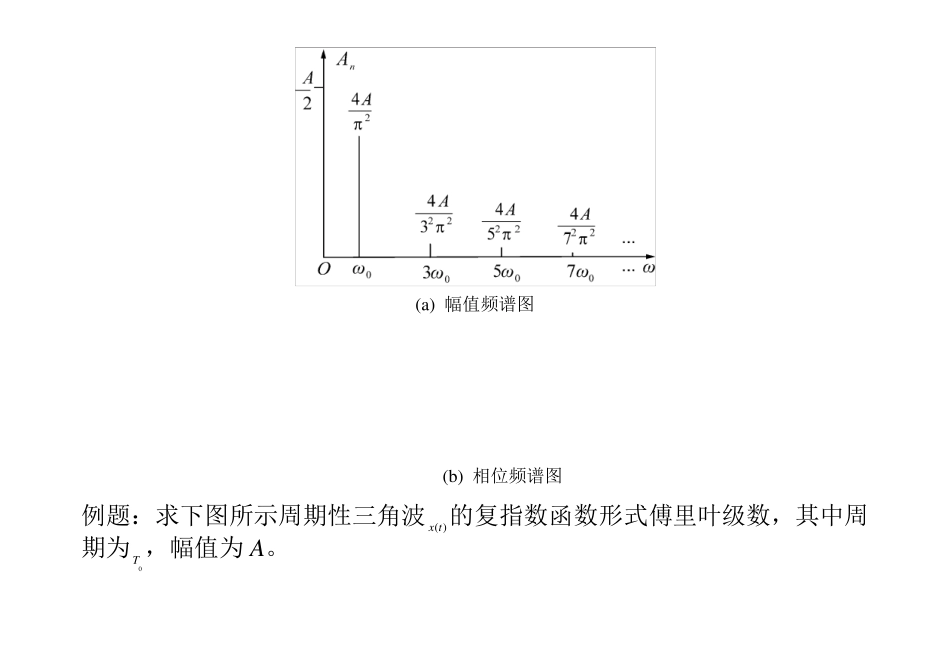
例题：求下图所示周期性三角波( )x t 的三角函数形式傅里叶级数，其中周期为0T ，幅值为A。 解：在( )x t 的一个周期中，( )x t 可表示为 0000(0)22( )(0)22TAAttTx tTAAttT ≤ ≤≤ ≤ 由于 ( )x t 为偶函数，故正弦分量幅值0nb。 常值分量 -T0/2 T0/2 A t x (t) 00/200/200111( )22TTAax t dtTATT而余弦分量幅值为 000/ 2/ 200/ 200002222222222( )cosd2()cosd41,3,5,24(cos1)sin202,4,6,TTnTAax tnt tAtnt tTTTAnnAAnnnnn   展开式为 000222411( )(coscos3cos5)235AAx tttt (a) 幅值频谱图 (b) 相位频谱图 例题：求下图所示周期性三角波( )x t 的复指数函数形式傅里叶级数，其中周期为0T ，幅值为A。 解：方法一： 在( )x t 的一个周期中，( )x t 可表示为 0000(0)22( )(0)22TAAttTx tTAAttT ≤≤≤≤ -T0/2 T0/2 A t x (t) 0( )0, 1, 2,jntnnx tC en  方法二： 在( )x t 的一个周期中，( )x t 可表示为 0000(0 )22( )(0)22TAAttTx tTAAttT ≤≤≤≤ 000/ 2/ 201( )0 , 1, 2 ,.......TjntnTCx t edtnT 0( )0 , 1, 2 ,jntnnx tC en  下面考虑n 取不等于0 的整数： 000/ 2/ 200/ 200002222222222( )cosd2()cosd41,3,5,24(cos1)sin202,4,6,TTnTAax tnt tAtnt tTTTAnnAAnnnnn   由于( )x t 为偶函数，故正弦分量幅值0nb。 从而， 1 ()2nnnCajb00/20000/20111( )/22TTCax t dtT A TAT 从而其复指数形式是 22221 421,3, 5,....11()22202,4, 6,....nnnnAAnCajbannn   2221, 3, 5,....02, 4, 6,..../ 2000, 1, 3, 5,....nnAnnCnAnn    0222( );1, 3, 5,2jntAAx tenn 从而幅频谱nC图是： 相频谱n图是： 注： 其中积分计算： 00000000001cossin1 [ sinsin]11[ sincos]tntdttdntntntntdtntntntCnn...