三常微分方程答案

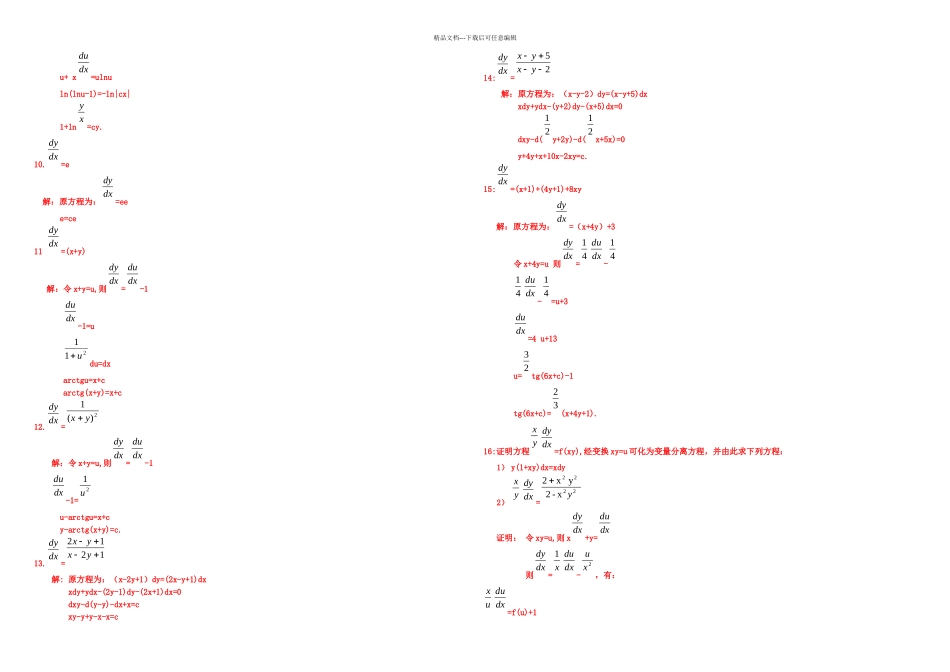
精品文档---下载后可任意编辑1．=2xy,并满足初始条件：x=0,y=1 的特解。解：=2xdx 两边积分有：ln|y|=x+cy=e+e=cex另外 y=0 也是原方程的解，c=0 时，y=0原方程的通解为 y= cex,x=0 y=1 时 c=1特解为 y= e.2. ydx+(x+1)dy=0 并求满足初始条件：x=0,y=1 的特解。 解：ydx=-(x+1)dy dy=-dx两边积分: -=-ln|x+1|+ln|c| y=另外 y=0,x=-1 也是原方程的解 x=0,y=1 时 c=e特解：y=3．= 解：原方程为：=dy=dx 两边积分：x(1+x)(1+y)=cx4. (1+x)ydx+(1-y)xdy=0 解：原方程为： dy=-dx两边积分：ln|xy|+x-y=c另外 x=0,y=0 也是原方程的解。5．（y+x）dy+(x-y)dx=0 解：原方程为：=-令=u 则=u+x 代入有：-du=dxln(u+1)x=c-2arctgu即 ln(y+x)=c-2arctg.6. x-y+=0 解：原方程为： =+-则令=u =u+ x du=sgnx dxarcsin=sgnx ln|x|+c7. tgydx-ctgxdy=0 解:原方程为：=两边积分：ln|siny|=-ln|cosx|-ln|c|siny== 另外 y=0 也是原方程的解，而 c=0 时，y=0.所以原方程的通解为 sinycosx=c.8 +=0 解：原方程为：=e2 e-3e=c.9.x(lnx-lny)dy-ydx=0 解：原方程为：=ln令=u ,则=u+ xdxdyydy2ydy11xy1|)1(|ln1xc|)1(|ln1xcdxdyyxxyy321dxdyyy 2131xx yy 2131xx yy1xx1dxdyyxyxxydxdydxdu112 uux12xydxdy22yx dxdyxyxx ||2)(1xyxydxdydxdu211ux1xytgydyctgxdxxccos1xccosdxdyyexy32 dxdyye y2dxdyxyxyxydxdydxdu精品文档---下载后可任意编辑u+ x=ulnuln(lnu-1)=-ln|cx|1+ln=cy.10.=e 解：原方程为：=eee=ce11 =(x+y) 解：令 x+y=u,则=-1-1=udu=dxarctgu=x+carctg(x+y)=x+c12.=解：令 x+y=u,则=-1-1= u-arctgu=x+c y-arctg(x+y)=c.13.=解: 原方程为：（x-2y+1）dy=(2x-y+1)dx xdy+ydx-(2y-1)dy-(2x+1)dx=0 dxy-d(y-y)-dx+x=c xy-y+y-x-x=c14:=解：原方程为：（x-y-2）dy=(x-y+5)dx xdy+ydx-(y+2)dy-(x+5)dx=0 dxy-d(y+2y)-d(x+5x)=0 y+4y+x+10x-2xy=c.15:=(x+1)+(4y+1)+8xy 解：原方程为：=（x+4y）+3令 x+4y=u 则=--=u+3=4 u+13u=tg(6x+c)-1tg(6x+c)=(x+4y+1).16:证明方程=f(xy),经变换 xy=u 可化为变量分离方程，并由此求下列方程：1） y(1+xy)dx=xdy2）= 证明： 令 xy=u,则 x+y= 则=-，有：=f(u)+1dxduxydxdydxdydxdydxdydxdudxdu211udxdy2)(1yx dxdydxdudxdu21udxdy1212yxyxdxdy25yxyx2121dxdydxdydxdy41dxdu4...