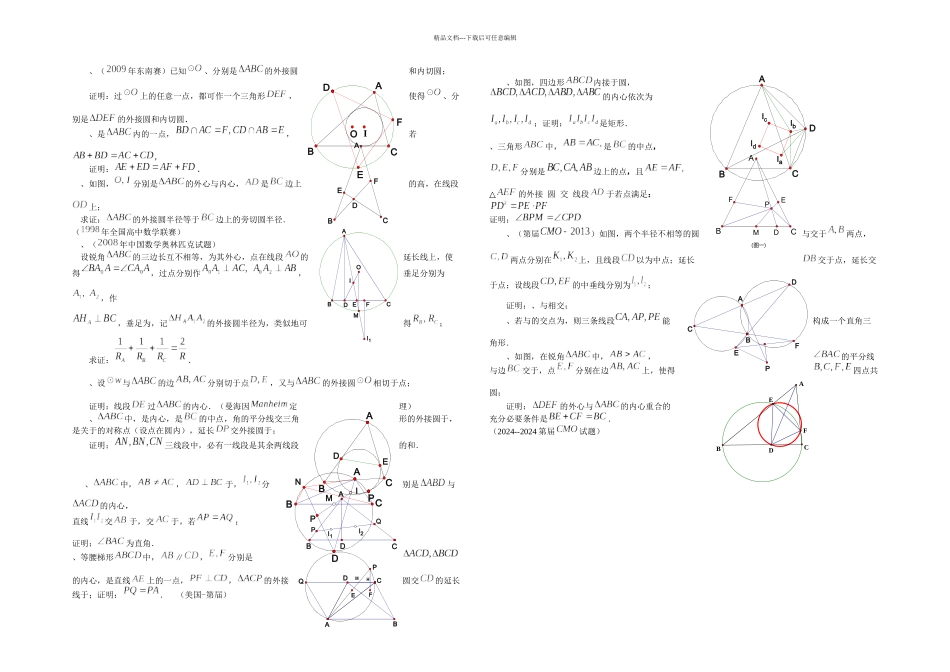
三角形的五心-A(角分线心)内心与旁心 陶平生三角形的五心是指内心、外心、重心、垂心与旁心;在数学竞赛中占有十分重要的位置.从赛题统计方面来看,其中又以角分线心的问题最为突出,必须熟悉其基本性质,基本构形,常用辅助线以及基本定理的应用.本讲座介绍内心与旁心问题的内心为,而边外的旁心分别为;分别是三条内角平分线,交三角形外接圆于,交外接圆于,交于,显然,三角形过同一顶点的内、外角平分线互相垂直,并且有、;、;、;;、;;、;、;(称为对称比定理).、,(俗称“鸡爪”定理).(注意,中最后一等式仅当外角分线与边有交点时使用)、中,是的平分线,点分别在上,满足,分别是的中点;证明:∥.、是直角三角形斜边上的高,(),分别是的内心,的外接圆分别交于,直线交于点;证明:分别是的内心与旁心.、四边形中,,自对角线的交点,作于,线段交于,交于,是线段上的任意一点.证明:点到线段的距离等于到线段、的距离之和.、的外心为,是的中点,直线交于,点分别是的外心与内心,若,证明:为直角三角形.、如图,四边形内接于,而与外切于点,且都内切于,若对角线分别是、的内、外公切线;证明:点是的内心.、如图,是所在平面上的一点,设点关于该三角形的三条内角平分线的对称点为;证明:三线共点.、(年全国高中数学联赛)内接于, 自作的切线, 又以为圆心,为半径作交直线于,交直线于;证明:四边形的四条边所在直线分别通过的内心及三个旁心.、中,是角平分线上的任一点,分别是延长线上的点,且∥,∥;若分别是的中点;证明:.、中,内切圆切于,设是的直径,若交于;证明:.KI1I3EI2DNFIMACBDNMQABCPPO1OBDO2CAI1I2I3IE2E1F1F2ABCD1M1M2M3D3D2MA2A1A3MNFEABCD精品文档---下载后可任意编辑、(年东南赛)已知、分别是的外接圆和内切圆;证明:过上的任意一点,都可作一个三角形,使得、分别是的外接圆和内切圆.、是内的一点,,若,证明:.、如图,分别是的外心与内心,是边上的高,在线段上;求证:的外接圆半径等于边上的旁切圆半径.(年全国高中数学联赛)、(年中国数学奥林匹克试题)设锐角的三边长互不相等,为其外心,点在线段的延长线上,使得,过点分别作,垂足分别为,作,垂足为,记的外接圆半径为,类似地可得;求证:.、设与的边分别切于点,又与的外接圆相切于点;证明:线段过的内心.(曼海因定理)、中,是内心,是的中点,角的平分线交三角形的外接圆于,是关于的对称...