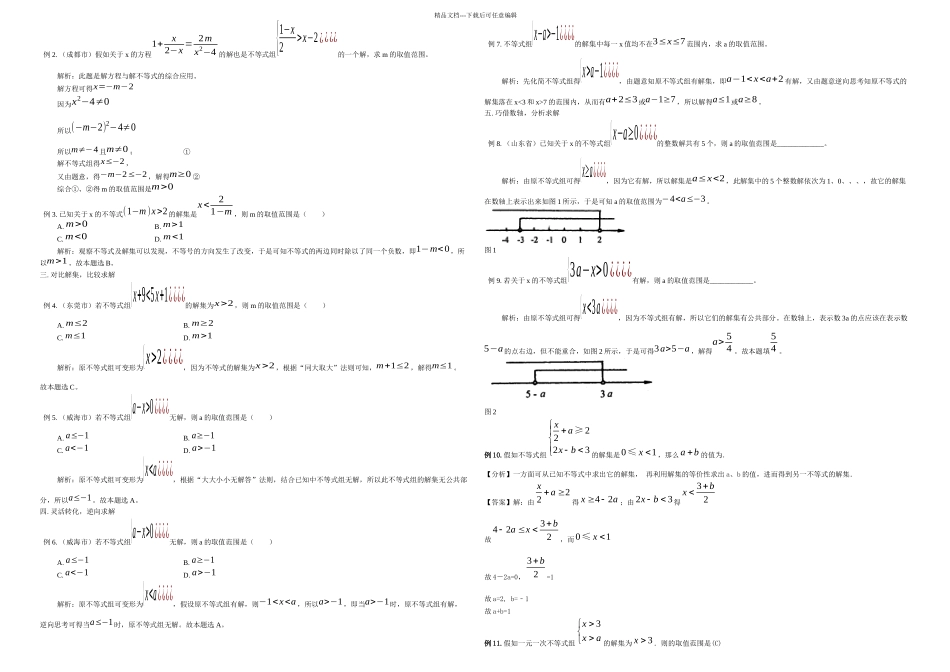
图 1a5a+3165743图 23m图 321m3m1m2图 4精品文档---下载后可任意编辑近年来各地中考、竞赛试题中,常常出现已知不等式(组)的解集,确定其中字母的取值范围的问题,下面举例说明字母取值范围的确定方法,供同学们学习时参考.一、 根据不等式(组)的解集确定字母取值范围 例 l、假如关于 x 的不等式(a+1)x>2a+2.的解集为 x<2,则 a 的取值范围是 ( ) A.a<0 B.a<一 l C.a>l D.a>一 l 解:将原不等式与其解集进行比较,发现在不等式的变形过程中运用了不等式的基本性质 3,因此有 a+l<0,得 a<一 1,故选 B. 例 2、已知不等式组的解集为 aa¿¿¿¿的整数解只有 5、6。求 a 和 b 的范围.解:解不等式组得{x>2+a¿¿¿¿,借助于数轴,如图 2 知:2+a 只能在 4 与 5 之间。b−12只能在 6 与 7 之间.4≤2+a<56<∴b−12≤72≤a<3∴,13一 l B.m>l C.m<一 1 D.m<1 分析:本题可先解方程组求出 x、y,再代入 x+y<0,转化为关于 m 的不等式求解;也可以整体思考,将两方程相加,求出 x+y 与 m 的关系,再由 x+y<0 转化为 m 的不等式求解. 解:(1)十(2)得,3(x+y)=2+2m,∴x+y=<0.∴m<一 l,故选 C. 例 6、(江苏省南通市 2024 年)已知 2a-3x+1=0,3b-2x-16=0,且 a≤4<b,求 x 的取值范围.解:由 2a-3x+1=0,可得 a=;由 3b-2x-16=0,可得 b=.又 a≤4<b,所以,≤4<,解得:-2<x≤3.四、逆用不等式组解集求解例 7、假如不等式组 无解,则 m 的取值范围是.分析:由 2x 一 6≥0 得 x≥3,而原不等式组无解,所以 3>m,∴m<3. 解:不等式 2x-6≥0 的解集为 x≥3,借助于数轴分析,如图 3,可知 m<3.例 8、不等式组{1