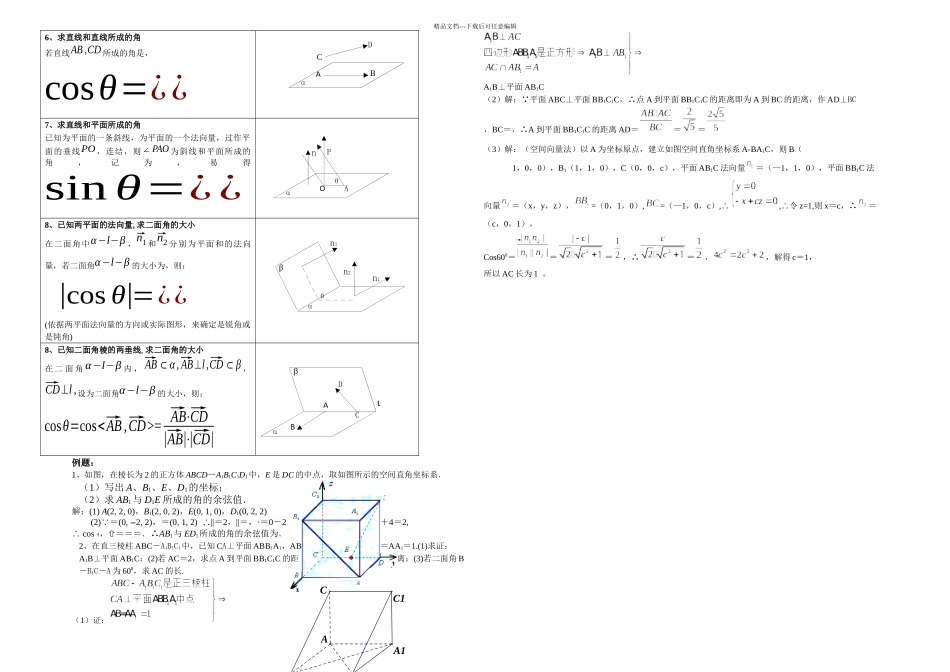
nBnBAαn2-11111n1-11111βαOPaFbEαnnPθOAα精品文档---下载后可任意编辑空间向量的有关概念和公式概念空间向量与平面对量的概念与性质相似,只是由二维平面拓展到三维空间假如一个向量所在直线垂直于一个平面,则该向量是这个平面的一个法向量。坐 标表示,, .运算则,,,,定 比分 点公式设点 P 分有向线段所成的比为 λ,即=λ,,,()中点公式:,,三角形重心公式:,,模,,则=√( x1−x2)2+( y1−y2)2+( z1−z2)2= ;= ;= ;=平行,(或==)垂直.()夹角cos ==●建立空间直角坐标系常用方法:1、底面是正方形,常以底面两条邻边为轴,轴;2、底面是菱形,常以底面两条对角线为轴,轴;3、底面是等腰三角形,常以底边及底边上的高为轴,轴;4、底面为平行四边形,常以一条边为轴,并作一条与这一条边垂直的直线作为轴。空间向量的应用(1)方法分类图形1、求平面的法向量若⃗AB=(x1, y1,z1),⃗AC=(x2, y2, z2),⃗AC∩⃗AB=A,⃗AB,⃗AC⊂α ,设⃗n=(x , y ,z)是平面的法向量,则{⃗n⋅⃗AB=0⃗n⋅⃗AC=0 ⇒{xx1+ yy1+zz1=0xx 2+ yy 2+ zz2=0(取x=x0 ,得到其中的一组解:⃗n=( x0 , y0, z0)而x0, y0, z0常取简单整数)2、证明线面平行设是平面的法向量,⃗AB⊄α ,则:⃗AB||α ⇔⃗AB⋅⃗n=03、证明面面垂直设⃗n1,⃗n2分别是平面α ,β 的法向量, 则:α ⊥ β⇔⃗n1⋅⃗n2=04、求两条异面直线间的距离先求两条异面直线的一个公共法向量,再求两条异面直线上两点的连结线段在公共法向量上的射影长设、是异面直线,是、的公共法向量,点E∈⃗a, F∈⃗b ,则异面直线、之间的距离d=|⃗EF⋅⃗n||⃗n|5、求点到平面的距离设为平面外一点,点为平面内的任一点,平面的法向量为,过点作平面的垂线PO ,记∠OPA=θ ,则点到平面的距离:d=|⃗PO|=|⃗PA|cosθ=|⃗PA|⋅|⃗n⋅⃗PA||⃗n|⋅|⃗PA|=|⃗n⋅⃗PA||⃗n|因此,点到平面的距离: d=|⃗n⋅⃗PA||⃗n|空间向量的应用(2)方法图形C1B1A1ABCADBCαnθPOAαn2n1n1θβαι βACDBα精品文档---下载后可任意编辑6、求直线和直线所成的角若直线AB,CD 所成的角是,cosθ=¿¿7、求直线和平面所成的角已知为平面的一条斜线,为平面的一个法向量,过作平面的垂线PO ,连结,则∠PAO 为斜线和平面所成的角,记为,易得sin θ=¿¿8、已知两平面的法向量, 求二面角的大小在二面角中α−l−β ,⃗n1 和⃗n2 分别为平面...