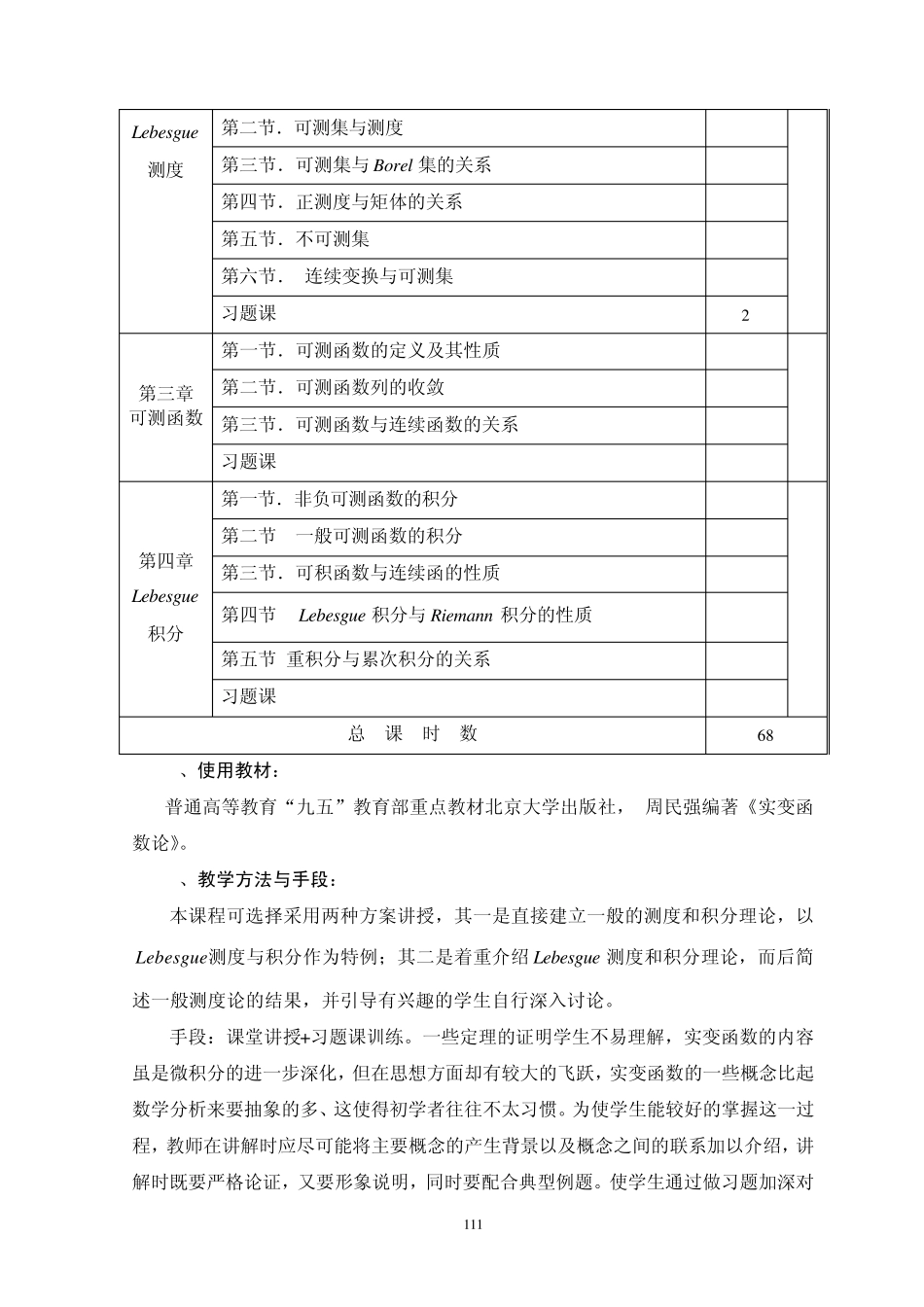
1 1 0 实变函数课程教学大纲 一、课程说明: 1、课程性质: 本课程是数学系基础课,为数学系本科学生所必修,也是微积分的进一步深化,这部分内容为学生进一步学习其它数学分支如泛函分析,函数论,微分方程,概率论„和科学研究提供必不可少的基础知识。 它是一学期课程,学时数的安排为: 一学期 68=174课时,其中习题课 17课时。 2、本课程的教学目的与要求: 通过实变函数这一学科的学习,应使学生较好的掌握测度与积分这个基本的数学工具,特别是极限与积分顺序的交换。并且在一定程度上掌握集的分析方法。 通过这门学科的教学,要加强对学生的抽象思维能力,逻辑推理能力的培养。在某些与中学教材相关的教学内容中,要引导学生在学习新知识的同时要加深对相关的中学教材的内容及背景的理解,使他们在今后的教学实践能用较高的观点处理中学教材。为培养成人师范学生较强的教学能力打下坚实的基础。 3、先行或后继课程: 实变函数是第五学期开设的专业必修课。是在数学分析的基础上发展而成,同时本课程又用到了高等代数和解几何中的一些基本知识。它的后继课程课有 概率统计、泛函分析、点集拓扑等。 4、教学时数分配表: 章 节 目 录 课时分配 第一章 集 合 与点集 第一节.集合与子集合 1 13 第二节.集合的运算 1 第三节.映射与基数 4 第四节.nR 中点与点之间的距离*点集的极限点 2 第五节.nR 中基本点集:闭集、开集、Borel 集、Cantor 集 4 第六节.*连续变换与可测集 1 (选学) 习题课 第二章 第一节.点集的 Lebesgu e 外测度 4 15 111 Lebesgue 测度 第二节.可测集与测度 4 第三节.可测集与Borel 集的关系 4 第四节.正测度与矩体的关系 1 第五节.不可测集 1 第六节.*连续变换与可测集 1 习题课 2 第三章 可测函数 第一节.可测函数的定义及其性质 4 16 第二节.可测函数列的收敛 8 第三节.可测函数与连续函数的关系 4 习题课 第四章 Lebesgue 积分 第一节.非负可测函数的积分 4 24 第二节 .一般可测函数的积分 6 第三节.可积函数与连续函的性质 2 第四节. Lebesgue 积分与Riemann 积分的性质 4 第五节.重积分与累次积分的关系 6 习题课 总 课 时 数 68 5、使用教材: 普通高等教育“九五”教育部重点教材北京大学出版社, 周民强编著《实变函数论》。 6、教学方法与手段: 本课程可选择采用两种方案讲授,...