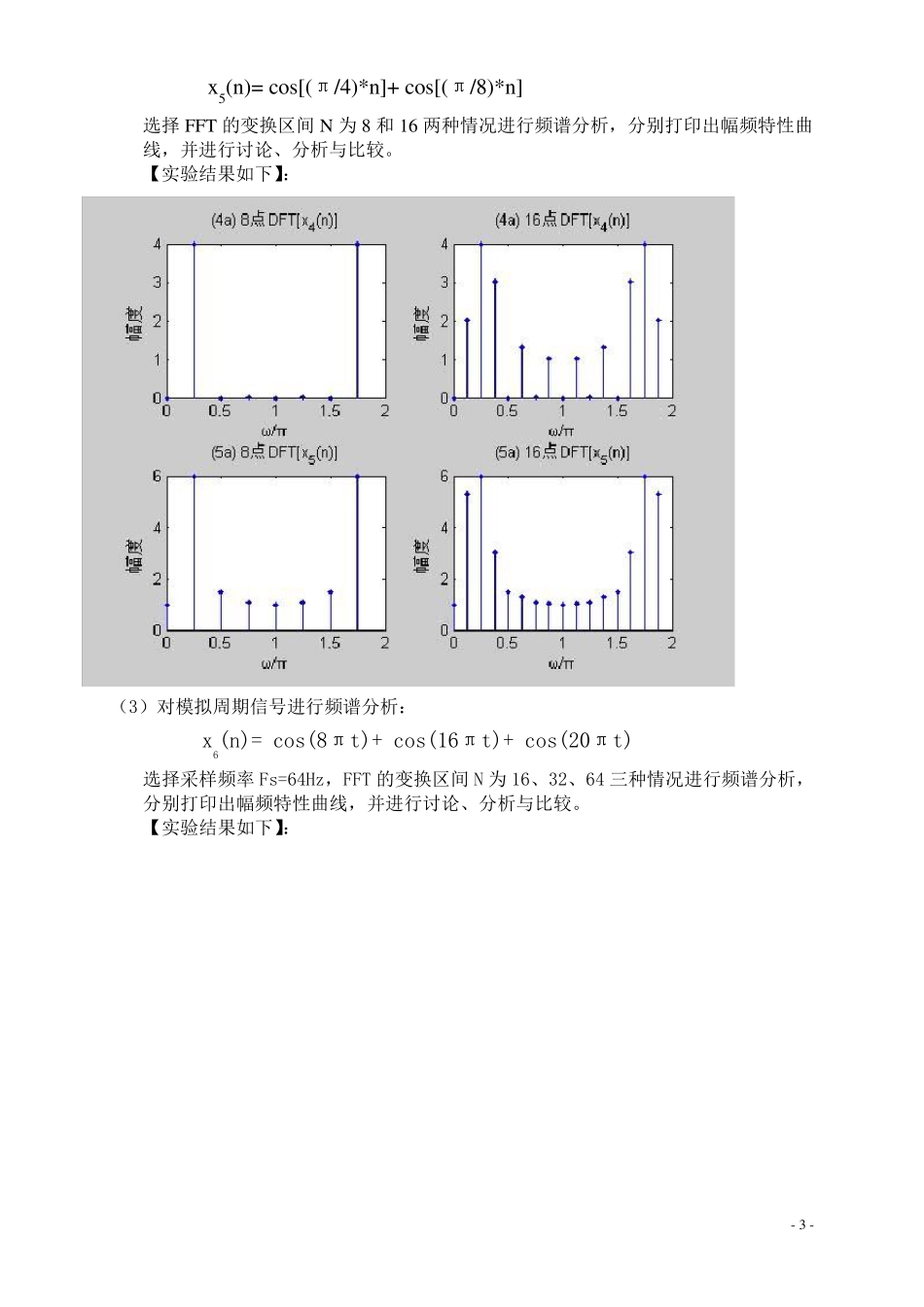
- 1 - 实验三:用 FFT 对信号作频谱分析实验报告 一、 实验目的与要求 学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便正确应用FFT。 二、 实验原理 用FFT 对信号作频分析是学习数字信号处理的重要内容,经常需要进行分析的信号是模拟信号的时域离散信号。对信号进行谱分析的重要问题是频谱分辨率D 和分析误差。频谱分辨率直接和FFT 的变换区间N 有关,因为FFT 能够实现的频率分辨率是2π/N,因此要求2π/N 小于等于 D。可以根据此式选择 FFT 的变换区间N。误差主要来自于用FFT 作频谱分析时,得到的是离散谱,而信号(周期信号除外)是连续谱,只有当 N 较大时,离散谱的包络才能逼近连续谱,因此N 要适当选择大一些。 三、 实验步骤及内容(含结果分析) (1)对以下序列进行FFT 分析: x1(n)=R4(n) x2(n)= x3(n)= 选择 FFT 的变换区间N 为8 和16 两种情况进行频谱分析,分别打印出幅频特性曲线,并进行讨论、分析与比较。 【实验结果如下】: n+1 0≤n≤3 8-n 4≤n≤7 0 其它 n 4-n 0≤n≤3 n-3 4≤n≤7 0 其它 n - 2 - 实验结果图形与理论分析相符。 (2)对以下周期序列进行谱分析: x 4(n)=cos[(π/4)*n] - 3 - x 5(n)= cos[(π/4)*n]+ cos[(π/8)*n] 选择 FFT 的变换区间 N 为 8 和 16 两种情况进行频谱分析,分别打印出幅频特性曲线,并进行讨论、分析与比较。 【实验结果如下】: (3)对模拟周期信号进行频谱分析: x6(n)= cos(8πt)+ cos(16πt)+ cos(20πt) 选择采样频率 Fs=64Hz,FFT 的变换区间 N 为 16、32、64 三种情况进行频谱分析,分别打印出幅频特性曲线,并进行讨论、分析与比较。 【实验结果如下】: - 4 - 四、 【附录】(实验中代码) x1n=[ones(1,4)]; %产生R4(n)序列向量 X1k8=fft(x1n,8); %计算x1n 的8 点DFT X1k16=fft(x1n,16); %计算x1n 的16 点DFT %以下绘制幅频特性曲线 N=8; f=2/N*(0:N-1); figure(1); subplot(1,2,1);stem(f,abs(X1k8),'.'); %绘制8 点DFT 的幅频特性图 title('(1a) 8 点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度'); N=16; f=2/N*(0:N-1); subplot(1,2,2);stem(f,abs(X1k16),'.'); %绘制8 点DFT 的幅频特性图 title('(1a) 16 点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度'); %x2n 和 x3n M=8;xa=1:(M/2);...