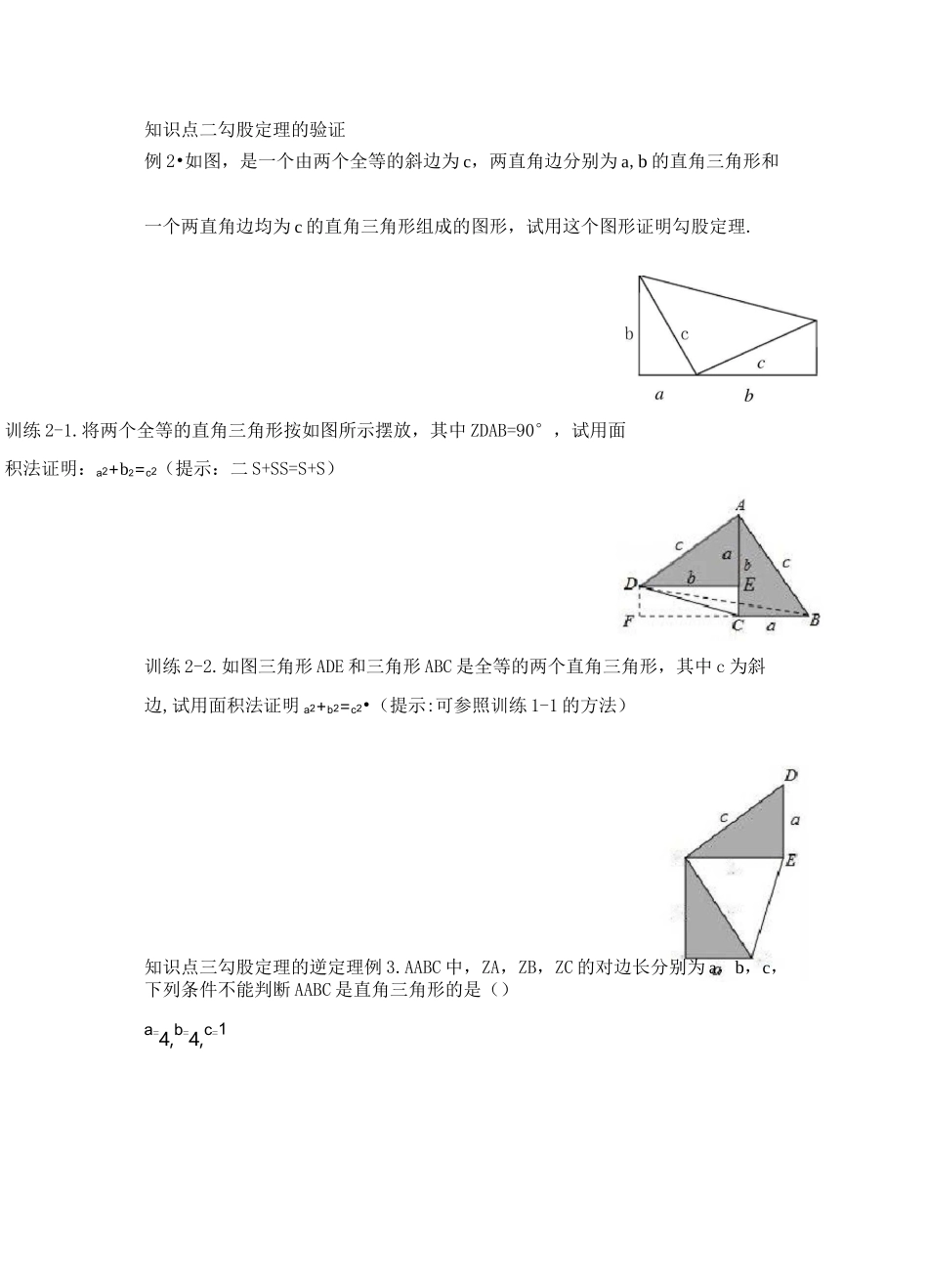
A.1cm,2cm,3cC.7c勾股定理及逆定理1.勾股定理的基本概念RtAABC 中,ZA,ZB,ZC 的对边长分别为 a,b,c 则 a2+b2=c2,a2=c2-b2,b2=c2-a2(c 为三角形的斜边)2.勾股定理的证明如图,小正方形的面积 c2=(a+b)2-abx4,化简即 a2+b2=c2.23. 勾股定理的逆定理如果一个三角形的三边满足 a2+b2=c2,a2=c2-b2,b2=c2-a2之一,那么这个三角形一定是直角三角形.4.勾股定理及逆定理的综合应用运用勾股定理及直角三角形的判别条件解决一些实际问题.例题精讲知识点一勾股定理的基本概念例 1•在 RtAABC 中,ZA=90°,ZA,ZB,ZC 的对边长分别为 a,b,c,那么下列等式一定成立的是()A.a2+b2=c2B.a2+c2=b2C.b2+c2=a2D.b2-c2=a2训练 1-1.下列四组数据均为三条线段的长度,其中能作为 RtAABC 三边的是()aA.ZA=ZC-ZBB.a:b:c 二 2:3:4C.a2=b2一 c2D.知识点二勾股定理的验证例 2•如图,是一个由两个全等的斜边为 c,两直角边分别为 a,b 的直角三角形和一个两直角边均为 c 的直角三角形组成的图形,试用这个图形证明勾股定理.训练 2-2.如图三角形 ADE 和三角形 ABC 是全等的两个直角三角形,其中 c 为斜边,试用面积法证明 a2+b2=c2•(提示:可参照训练 1-1 的方法)知识点三勾股定理的逆定理例 3.AABC 中,ZA,ZB,ZC 的对边长分别为 a,b,c,下列条件不能判断 AABC 是直角三角形的是()a=4,b=4,c=1训练 2-1.将两个全等的直角三角形按如图所示摆放,其中 ZDAB=90°,试用面积法证明:a2+b2=c2(提示:二 S+SS=S+S)四边形 ADCB△ACD△ABC,四边形 ADCB△ADB△DCB训练 4-1.如图:一个长、宽、高分别为 4cm、3cm、12cm 的长方体盒子能容下A.11cmB.12cmC.13cmD.14cm训练 3-1.已知 a,b,c 是二角形的二边长,如果满足(a-6)2+Jb-8+c—10—0,那么下列说法中不正确的是()A.这个三角形是直角三角形 B.这个三角形的最长边长是 10C.这个三角形的面积是 48D.这个三角形的最长边上的高是 4.8训练 3-2.若 a,b,c 是△ABC 的三条边,且满足 a2—2ab+b2=0,(a+b)2=2ab+c2,则△ABC 的形状为()A.锐角三角形 B.钝角三角形 C.等边三角形 D.等腰直角三角形知识点四勾股定理及逆定理的应用例 4.如图,将一根长 24cm 的筷子,置于底面直径为 5cm,高为 12cm 的圆柱形水杯中,设筷子露在杯子外面的长度为 hem,则 h 的取值范围是()A.12cmWhW19cmB.12cmWhW13cmC.llcmWhW12cmD.5cmWhW12cm训练 4-2.如图,在波平如镜的湖面上,有一...