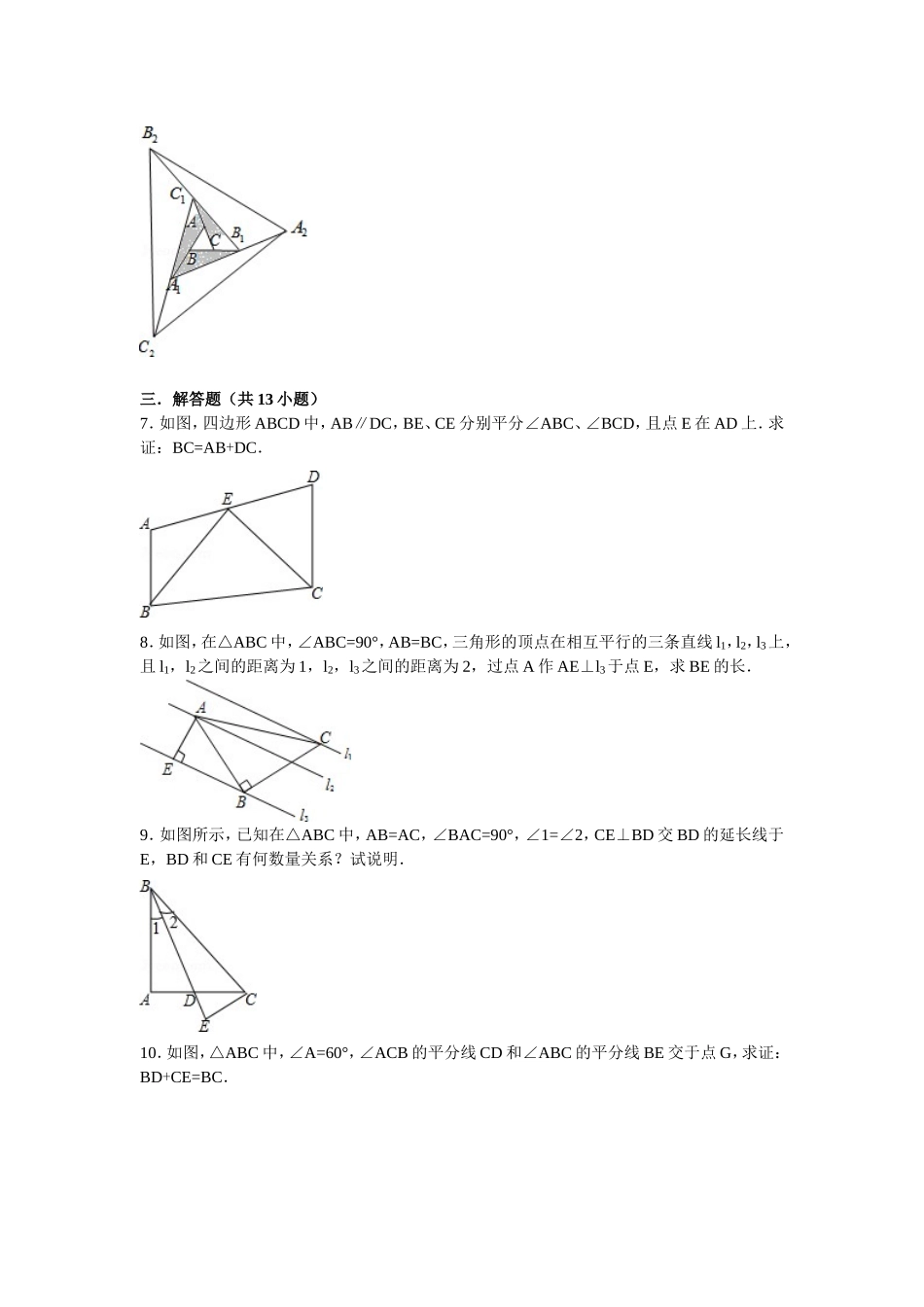
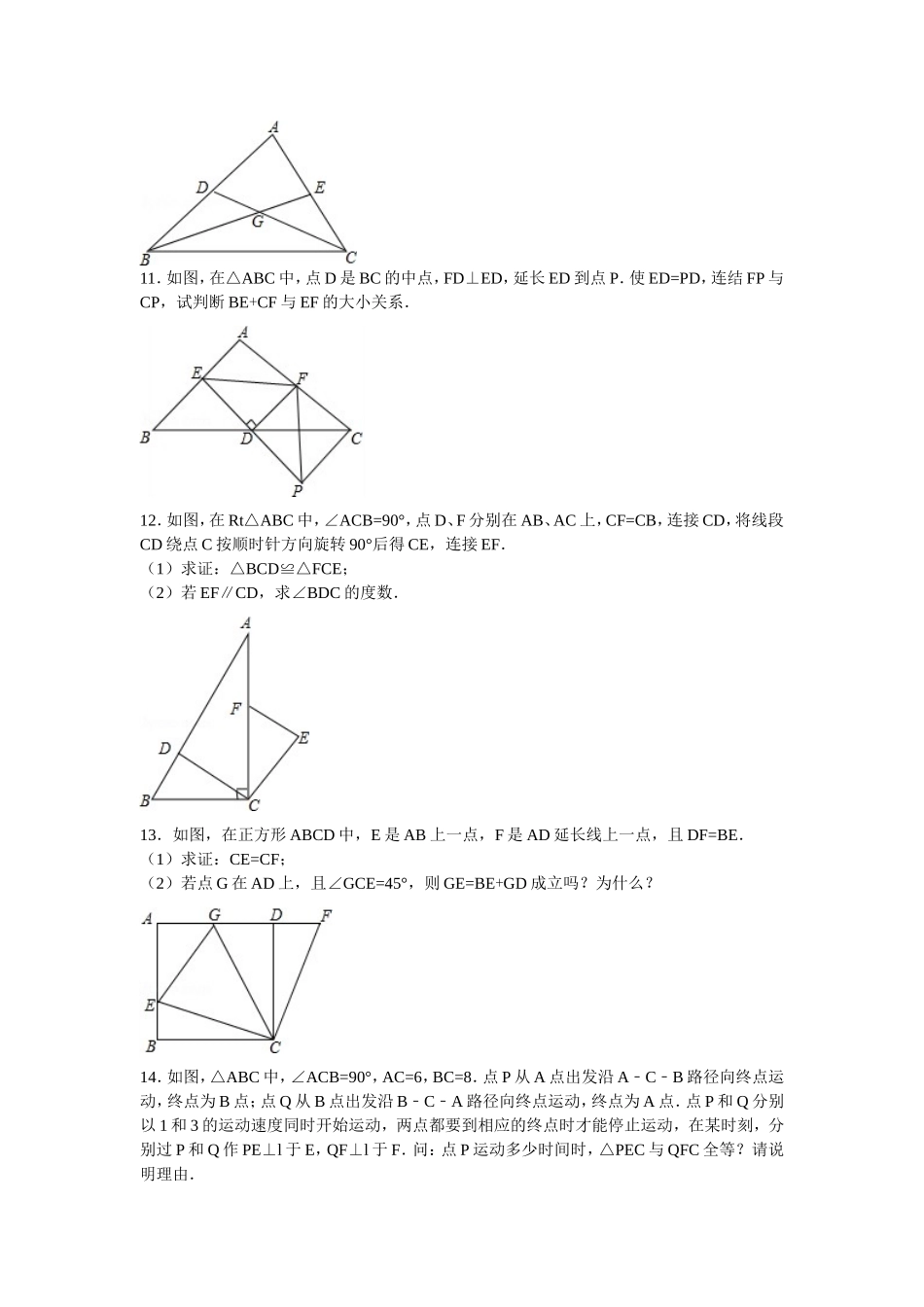
初二数学组卷一.选择题(共2小题)1.定义运算符号“﹡”的意义为:ab=﹡(其中a、b均不为0).下面有两个结论:(1)运算“﹡”满足交换律;(2)运算“﹡”满足结合律.其中()A.只有(1)正确B.只有(2)正确C.(1)和(2)都正确D.(1)和(2)都不正确2.下列说法正确的是()A.三角形的角平分线,中线和高都在三角形的内部B.直角三角形的高只有一条C.钝角三角形的三条高都在三角形外D.三角形的高至少有一条在三角形内二.填空题(共4小题)3.如图,△ABC的角平分线AD、BE交于点F,点F到边BC的距离为2cm,那么点F到边AC的距离为cm.4.如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于.5.“若a<0,b<0,则ab<0”,这个命题的题设是,结论是.6.如图,将△ABC第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1、B1、C1,得到△A1B1C1,第二次操作:分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2、B2、C2,得到△A2B2C2…按此规律,若△A3B3C3的面积是686,则△ABC的面积为.三.解答题(共13小题)7.如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上.求证:BC=AB+DC.8.如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,过点A作AE⊥l3于点E,求BE的长.9.如图所示,已知在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于E,BD和CE有何数量关系?试说明.10.如图,△ABC中,∠A=60°,∠ACB的平分线CD和∠ABC的平分线BE交于点G,求证:BD+CE=BC.11.如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系.12.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.(1)求证:△BCD≌△FCE;(2)若EF∥CD,求∠BDC的度数.13.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?14.如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿ACB﹣﹣路径向终点运动,终点为B点;点Q从B点出发沿BCA﹣﹣路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.15.如图所示,已知△ABC≌△ADE,BC的延长线交AD于点F,交DE于点G,且∠CAD=25°,∠B=∠D=30°,∠EAB=125°,求∠DFB和∠DGB的度数.16.(1)如图,已知△ABC中,AD⊥BC于D,AE为∠BAC的平分线,∠B=50°,∠C=70°,求∠DAE的度数.(2)已知在△ABC中,AD⊥BC于点D,AE平分∠BAC(∠C>∠B).求证:∠DAE=(∠C﹣∠B).17.如图:(1)CE∥AB,所以∠1=∠,∠2=∠.所以∠ACD=∠1+∠2=.(2)在图2中过点A作AE∥CD,交BC于点E;(3)请用(1)中这个结论,在图(2)中求出∠BAD+∠B+∠C+∠D的度数.18.已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.19.如图:在△ABC中,AB=AC,P为BC边上任意一点,PE⊥AB于E,PF⊥AC于F,若AC边上的高BD=a.(1)试证明:PE+PF=a;(2)若点P在BC的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE,PF,a的关系式,直接写出结论不需要说明理由.答案一.选择题(共2小题)1.定义运算符号“﹡”的意义为:ab=﹡(其中a、b均不为0).下面有两个结论:(1)运算“﹡”满足交换律;(2)运算“﹡”满足结合律.其中()A.只有(1)正确B.只有(2)正确C.(1)和(2)都正确D.(1)和(2)都不正确【考点】有理数的混合运算.菁优网版权所有【专题】新定义.【分析】本题可依据题意进行分析,ab=...