机械振动课后习题和答案第三章习题和答案

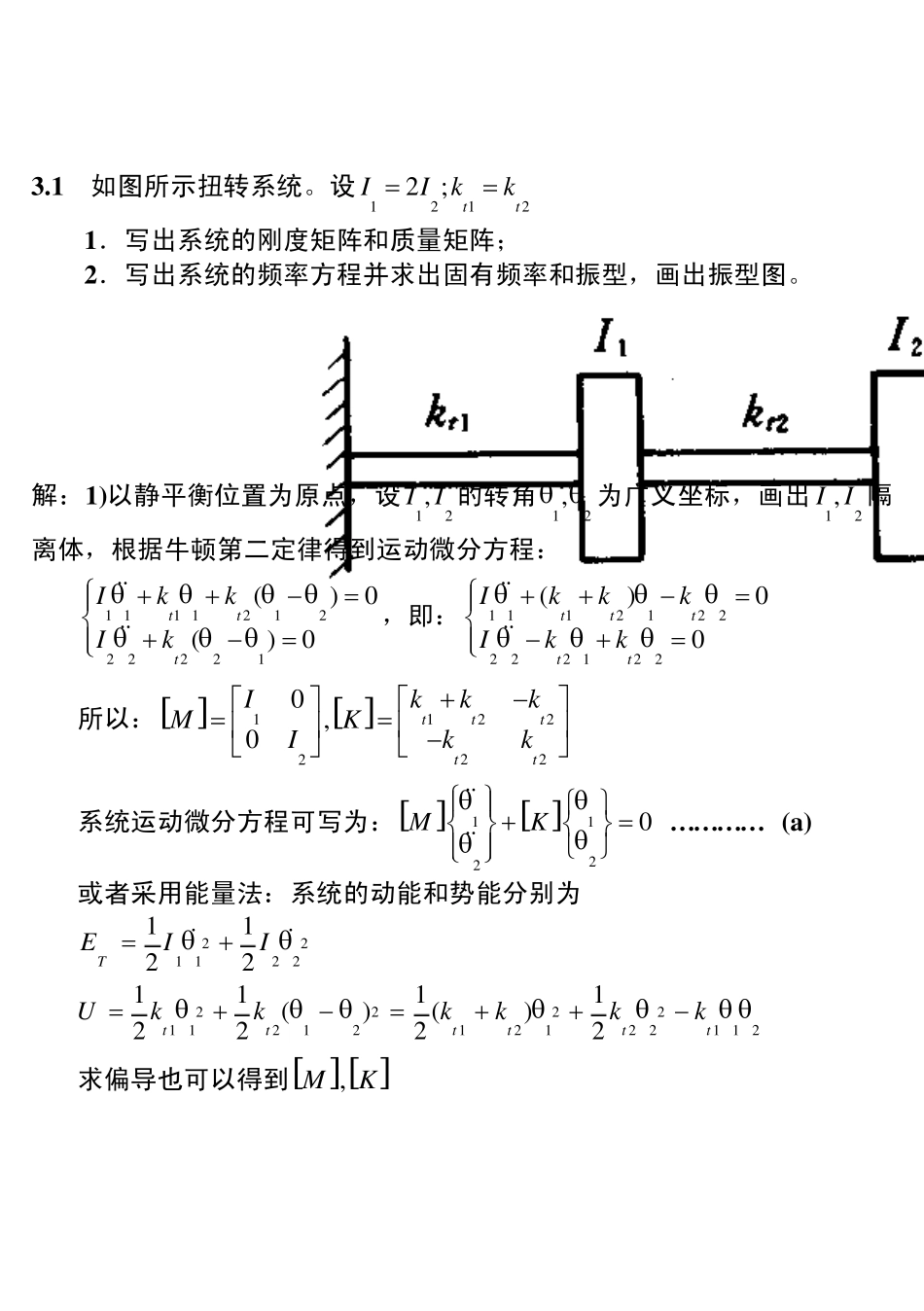
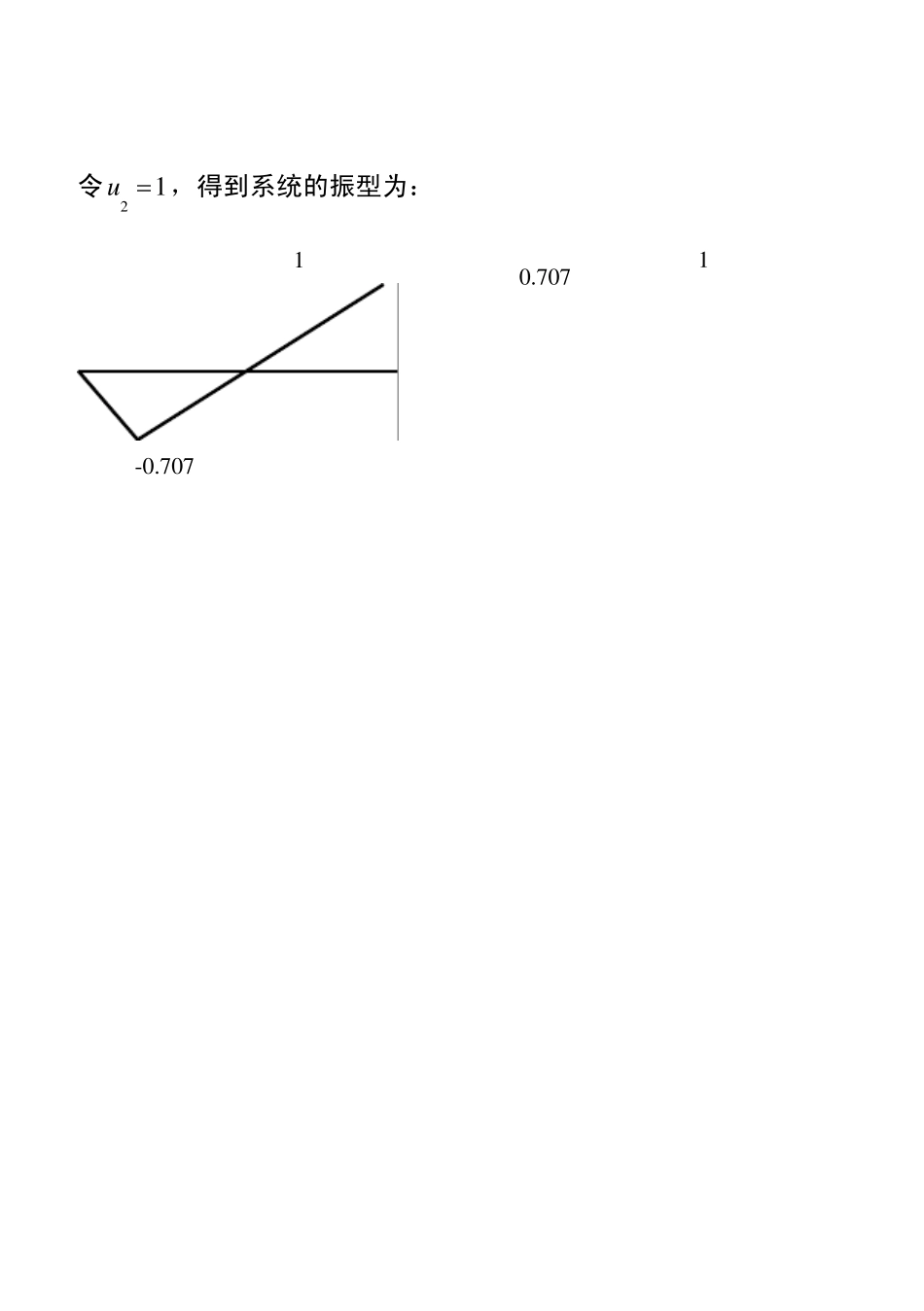
3 .1 如图所示扭转系统。设12122;ttIIkk 1 ．写出系统的刚度矩阵和质量矩阵； 2 ．写出系统的频率方程并求出固有频率和振型，画出振型图。 解：1 )以静平衡位置为原点，设12,I I 的转角12,  为广义坐标，画出12,I I 隔离体，根据牛顿第二定律得到运动微分方程： 1 11 121222221()0()0tttIkkIk，即：1 112122222 122()00tttttIkkkIkk 所以：  12212220 ,0tttttkkkIMKkkI  系统运动微分方程可写为：  11220MK  ………… (a ) 或者采用能量法：系统的动能和势能分别为 221 1221122TEII  222211212121221121111()()2222ttttttUkkkkkk 求偏导也可以得到   ,MK 由于12122;ttIIkk，所以  212021,0111tMIKk 2)设系统固有振动的解为： 1122cosutu，代入（a）可得：   122()0uKMu … … … … (b) 得到频率方程：22121211222()0ttttkIkkkI 即：2242221 21()240ttIk Ik 解得：2221 21 221211,22224(4)4 2(22)42ttttk Ik IIkkII  所以：112(22)2tkI<122(22)2tkI … … … … (c) 将（c）代入（b）可得： 112121211122(22)2220(22)2ttttttkkIkIuukkkII  解得：112122uu ；122222uu 令21u  ，得到系统的振型为： -0 .7 0 7 1 0 .7 0 7 1 3 .2 求图所示系统的固有频率和振型。设123213;33mm kkk。并画出振型图。 解：1 )以静平衡位置为原点，设12,m m 的位移12,x x 为广义坐标，画出12,m m 隔离体，根据牛顿第二定律得到运动微分方程： 1 11 12122222132()0()0m xk xkxxm xkxxk x 所以：  122122320,0kkkmMKkkkm  系统运动微分方程可写为：  11220xxMKxx … … … … (a) 或者采用能...