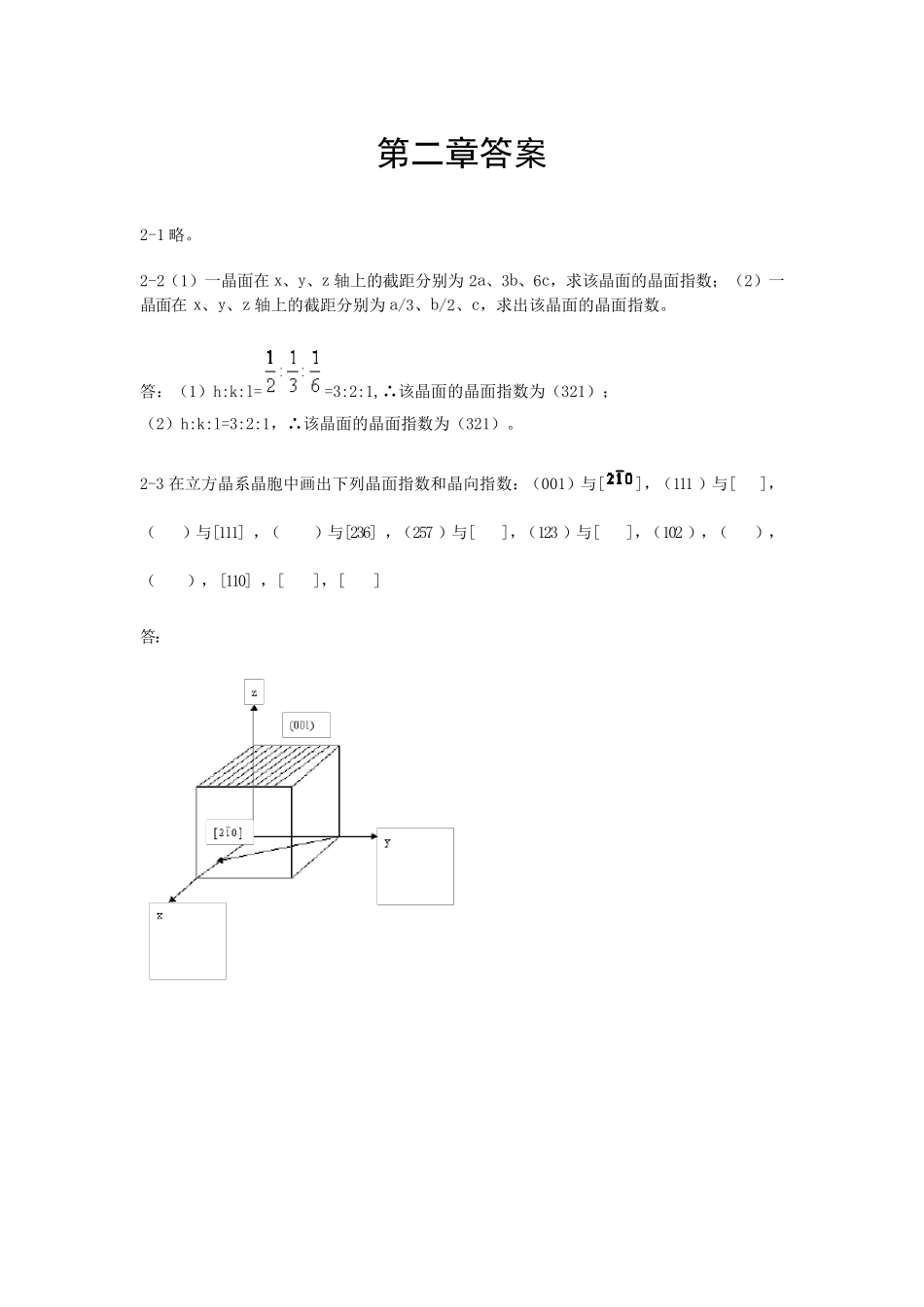
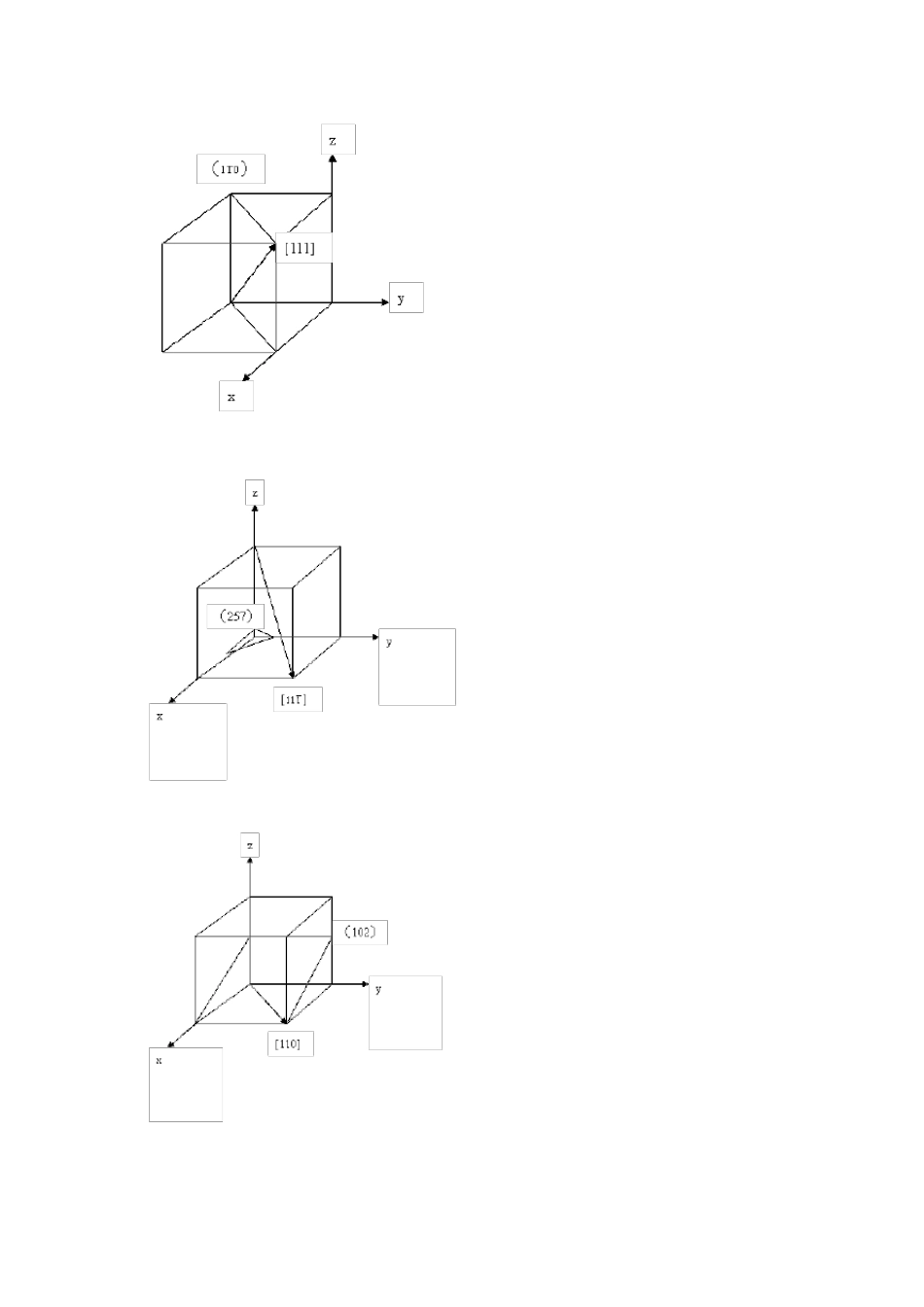
第二章答案 2-1 略。 2-2(1)一晶面在x、y、z 轴上的截距分别为2a、3b、6c,求该晶面的晶面指数;(2)一晶面在x、y、z 轴上的截距分别为a/3、b/2、c,求出该晶面的晶面指数。 答:(1)h:k:l==3:2:1,∴该晶面的晶面指数为(321); (2)h:k:l=3:2:1,∴该晶面的晶面指数为(321)。 2-3 在立方晶系晶胞中画出下列晶面指数和晶向指数:(001)与[],(111 )与[],()与[111] ,()与[236] ,(257 )与[],(123 )与[],(102 ),(),(),[110] ,[],[] 答: 2-4 定性描述晶体结构的参量有哪些?定量描述晶体结构的参量又有哪些? 答:定性:对称轴、对称中心、晶系、点阵。定量:晶胞参数。 2-5 依据结合力的本质不同,晶体中的键合作用分为哪几类?其特点是什么? 答:晶体中的键合作用可分为离子键、共价键、金属键、范德华键和氢键。 离子键的特点是没有方向性和饱和性,结合力很大。共价键的特点是具有方向性和饱和性,结合力也很大。金属键是没有方向性和饱和性的的共价键,结合力是离子间的静电库仑力。范德华键是通过分子力而产生的键合,分子力很弱。氢键是两个电负性较大的原子相结合形成的键,具有饱和性。 2-6 等径球最紧密堆积的空隙有哪两种?一个球的周围有多少个四面体空隙、多少个八面体空隙? 答:等径球最紧密堆积有六方和面心立方紧密堆积两种,一个球的周围有8 个四面体空隙、6 个八面体空隙。 2-7n 个等径球作最紧密堆积时可形成多少个四面体空隙、多少个八面体空隙?不等径球是如何进行堆积的? 答:n 个等径球作最紧密堆积时可形成 n 个八面体空隙、2n 个四面体空隙。 不等径球体进行紧密堆积时,可以看成由大球按等径球体紧密堆积后,小球按其大小分别填充到其空隙中,稍大的小球填充八面体空隙,稍小的小球填充四面体空隙,形成不等径球体紧密堆积。 2-8 写出面心立方格子的单位平行六面体上所有结点的坐标。 答:面心立方格子的单位平行六面体上所有结点为:(000)、(001)(100)(101)(110)(010)(011)(111)(0)(0)(0)(1)(1)(1)。 2-9 计 算 面 心 立 方 、 密 排 六 方 晶 胞 中 的 原 子 数 、 配 位 数 、 堆 积 系 数 。 答 : : 面 心 : 原 子 数 4, 配 位 数 6, 堆 积 密 度 六 方 : 原 子 数 6, 配 位 数 6, 堆 积 密 度 2-10 根 据 最 紧 密 堆 积...