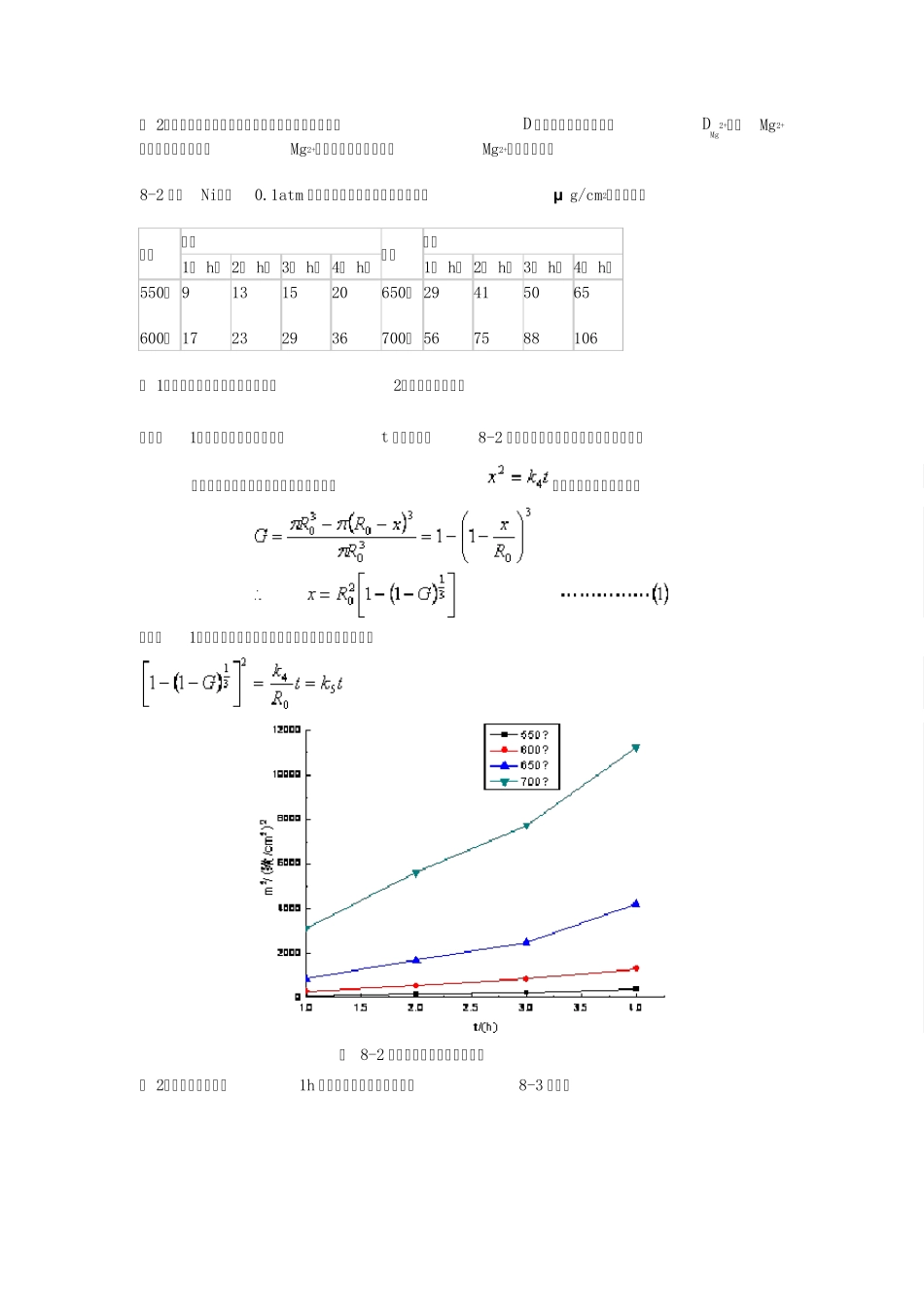
第八章答案 8-1 若由MgO 和 Al2O3球形颗粒之间的反应生成MgAl2O4是通过产物层的扩散进行的,(1)画出其反应的几何图形,并推导出反应初期的速度方程。(2)若1300℃时DAl3+ > DMg2+ , O2- 基本不动,那么哪一种离子的扩散控制着MgAl2O4的生成?为什么? 解:(1)假设: a)反应物是半径为R0的等径球粒B, x 为产物层厚度。 b)反应物A 是扩散相,即A 总是包围着B 的颗粒,且A, B 同产物C 是完全接触的,反应自球表面向中心进行。 c) A 在产物层中的浓度梯度是线性的,且扩散截面积一定。 反应的几何图形如图8-1 所示: 根据转化率G 的定义,得 将(1)式代入抛物线方程中,得反应初期的速度方程为: ( 2)整个反应过程中速度最慢的一步控制产物生成。D 小的控制产物生成,即DMg2+小,Mg2+扩散慢,整个反应由Mg2+的扩散慢,整个反应由Mg2+的扩散控制。 8-2 镍(Ni)在0.1atm 的氧气中氧化,测得其质量增量(μ g/cm2)如下表: 温度 时间 温度 时间 1( h) 2( h) 3( h) 4( h) 1( h) 2( h) 3( h) 4( h) 550℃ 600℃ 9 17 13 23 15 29 20 36 650℃ 700℃ 29 56 41 75 50 88 65 106 ( 1)导出合适的反应速度方程;(2)计算其活化能。 解:(1)将重量增量平方对时间t 作图,如图8-2 所示。由图可知,重量增量平方与时间呈抛物线关系,即符合抛物线速度方程式。又由转化率的定义,得 将式(1)代入抛物线速度方程式中,得反应速度方程为: 图 8-2 重量增量平方与时间关系图 ( 2)取各温度下反应1h 时进行数据处理拟合,如图8-3 所示, T(℃) G(%) 1/T (×10-3K-1) ln[1-(1-G)1/3] 550 9 1.22 -3.475 600 17 1.14 -2.810 650 29 1.08 -2.227 700 56 1.03 -1.430 图 8-3 数据处理 由杨德尔方程可得, 对数据作线性回归,得(相关系数为0.98839) 由上式得活化能kJ/mol 8-3 由 Al2O3和 SiO2粉末反应生成莫来石,过程由扩散控制,如何证明这一点?已知扩散活化能为209kJ/mol,1400℃下,1h 完成10%,求1500℃下,1h 和 4h 各完成多少?(应用杨德方程计算) 解:如果用杨德尔方程来描述Al2O3和 SiO2粉末反应生成莫来石,经计算得到合理的结果,则可认为此反应是由扩散控制的反应过程。 由杨德尔方程,得 又,故 从而1500℃下,反应1h 和 4h 时,由杨德尔方程,知 所以,在1500℃下反应1h...