柴俊,丁大公,陈咸平等编科学出版社华东师范大学高等数学作业集答案Ch_7

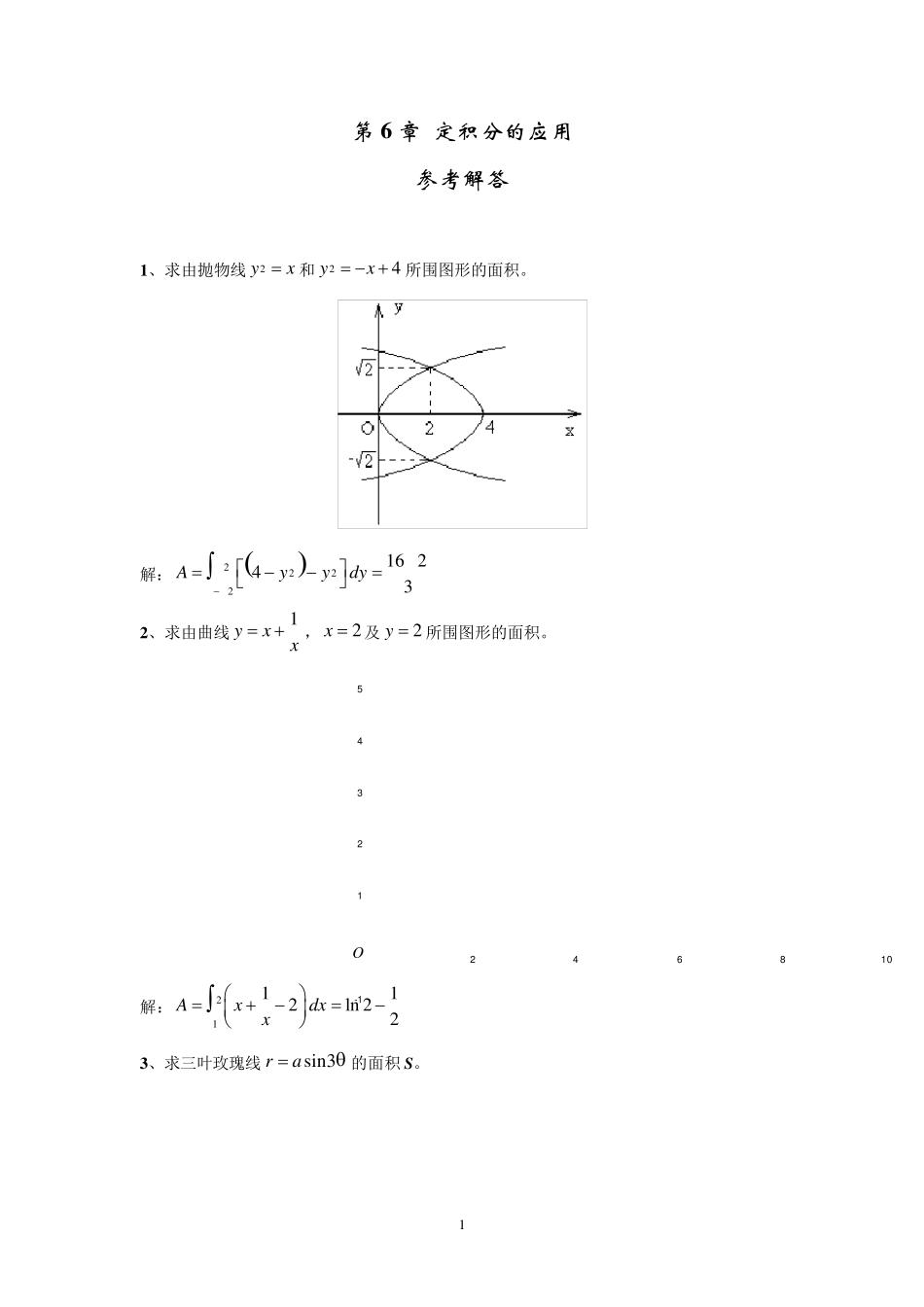
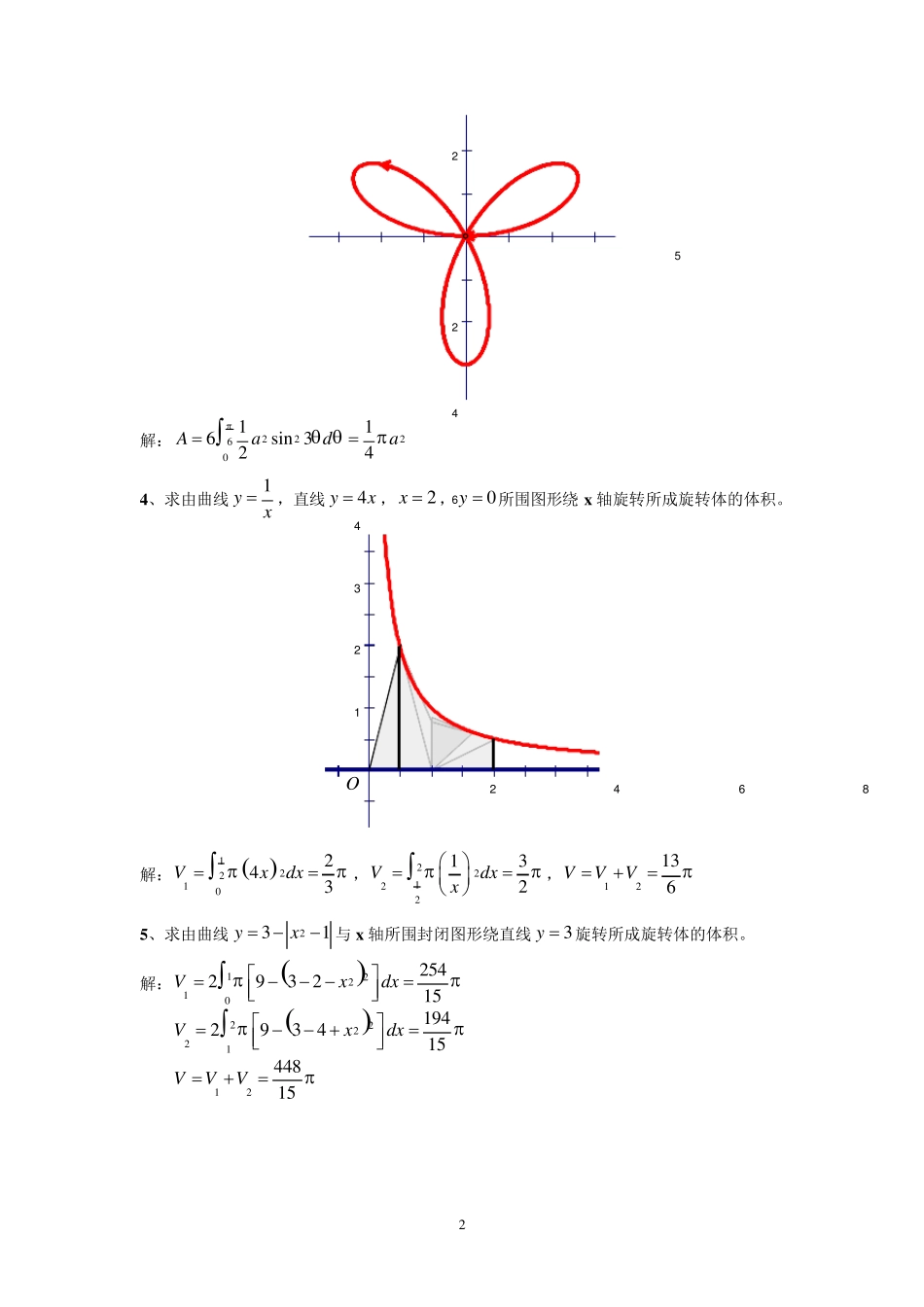
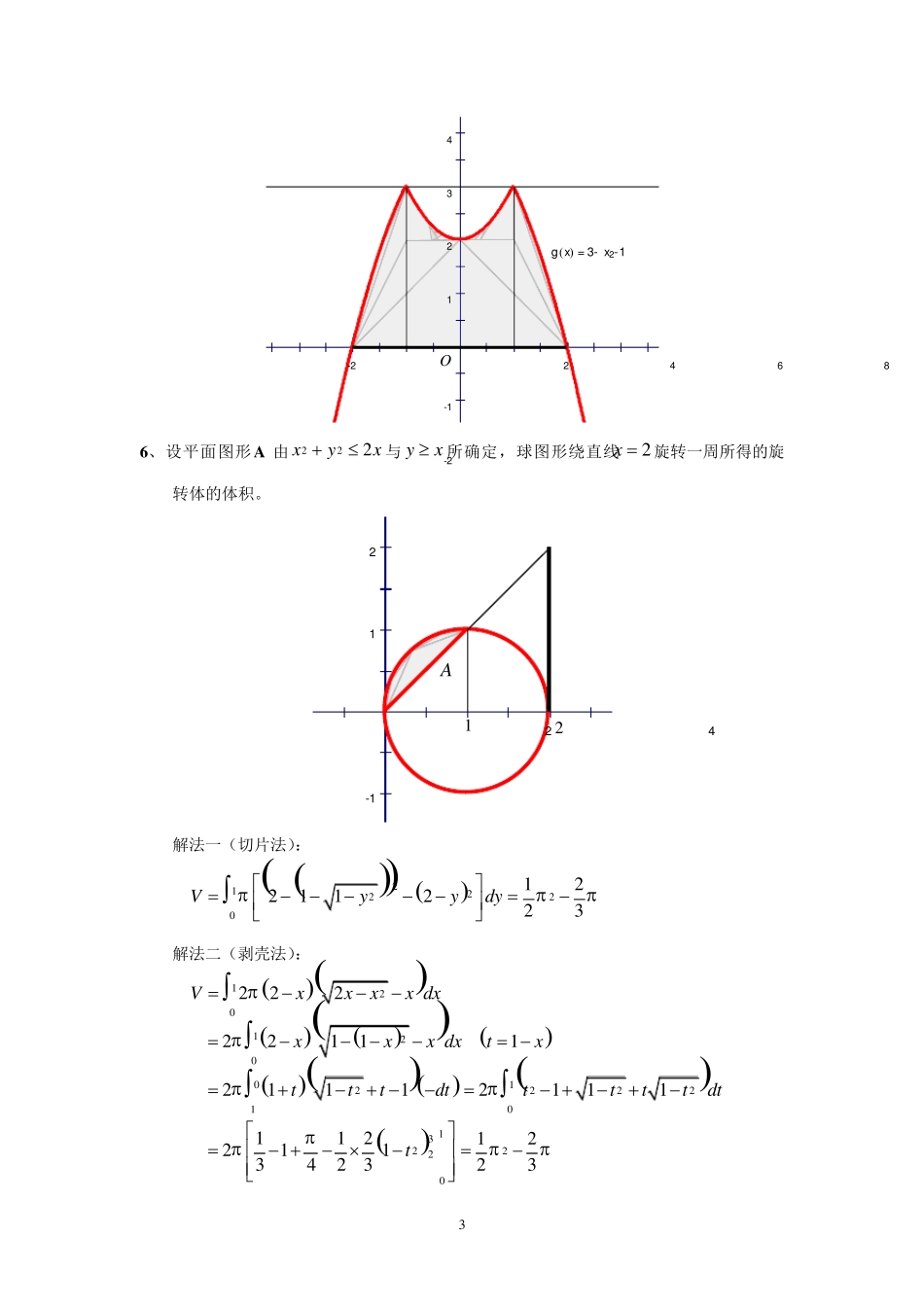
1 第 6 章 定积分的应用 参考解答 1 、求由抛物线2yx和24yx  所围图形的面积。 解：222216 243Ayydy 2 、求由曲线1yxx，2x 及2y 所围图形的面积。 54321-124681 0O 解：21112ln 22Axdxx 3 、求三叶玫瑰线sin3ra的面积 S。 2 22465 解：22260116sin 324Aada  4 、求由曲线1yx，直线4yx，2x ，0y 所围图形绕 x 轴旋转所成旋转体的体积。 43212468O 解：12210243Vxdx，22122132Vdxx，12136VVV 5 、求由曲线231yx与 x 轴所围封闭图形绕直线3y 旋转所成旋转体的体积。 解：12210254293215Vxdx 22221194293415Vxdx 1244815VVV 3 4321-1-2-22468g x  = 3- x2-1O 6、设平面图形A 由222xyx与 yx所确定，球图形绕直线2x 旋转一周所得的旋转体的体积。 21-12421A 解法一（切片法）：  21222012211223Vyydy 解法二（剥壳法）： 120222Vxxxx dx 12022111xxx dxtx  0212111tttdt 122202111ttttdt  132201122113423t  21223 4 7 、求曲线2ln 1yx上相应于102x的一段弧的弧长。 解：1211222222000211111lnln311122xxxsdxdxxxx 8 、求曲线44cos02sinxattyat  的弧长。 解： 2233204 cossin4 sincossattattdt  244204 sin cossincosatttt dt 22204 sin cos1 2sincosatttt dt 22012 sin 21sin 22att dt 220112 sin 2cos 222att dt 2202sin 21cos 22att dt 1211cos22axdxxt  12021axdx（利用分部积分或换元法）  122021ln12 a xxxx 22ln 122 a  9 、求曲线11cos22r的弧长。 解：  2222srrd...