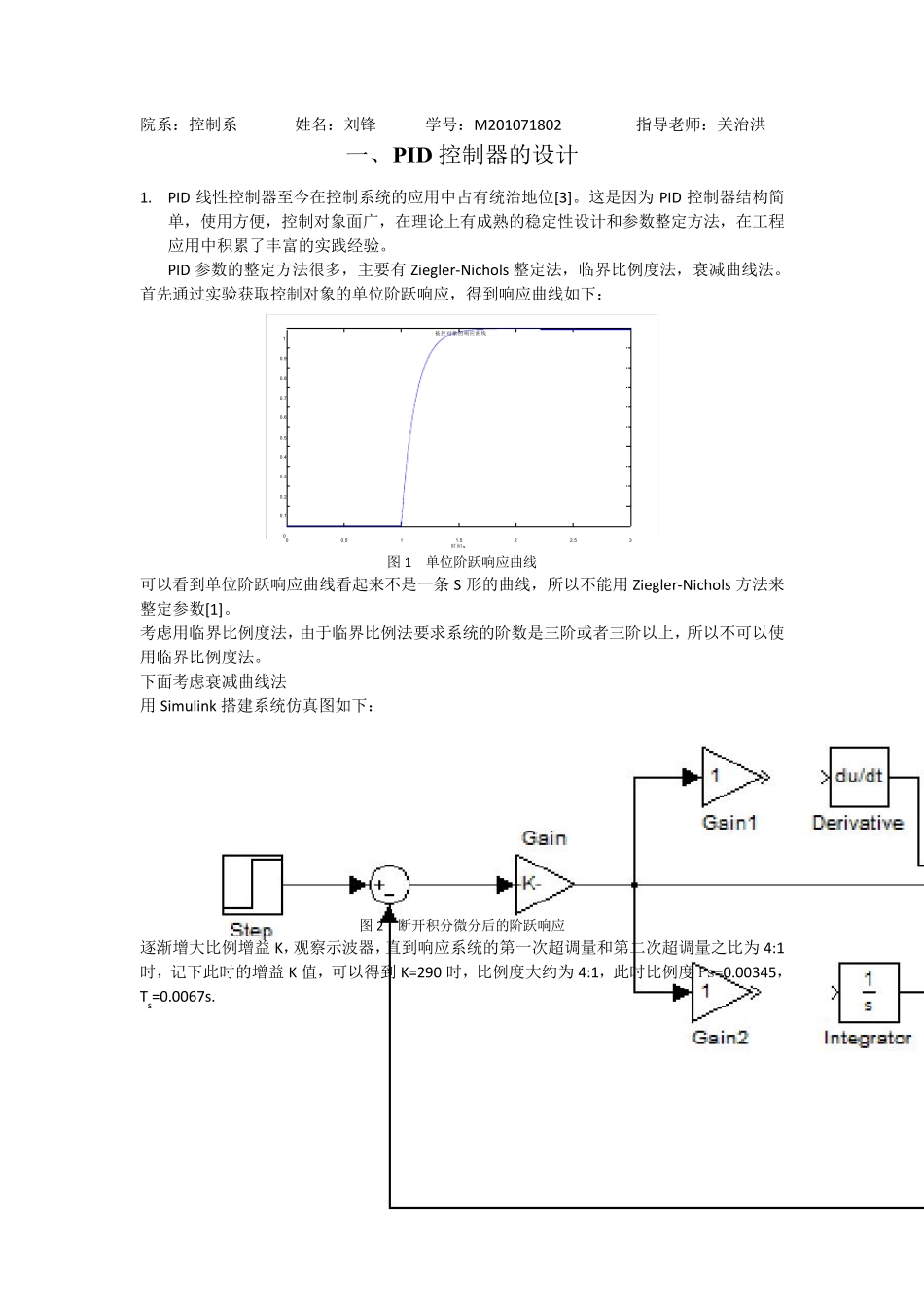
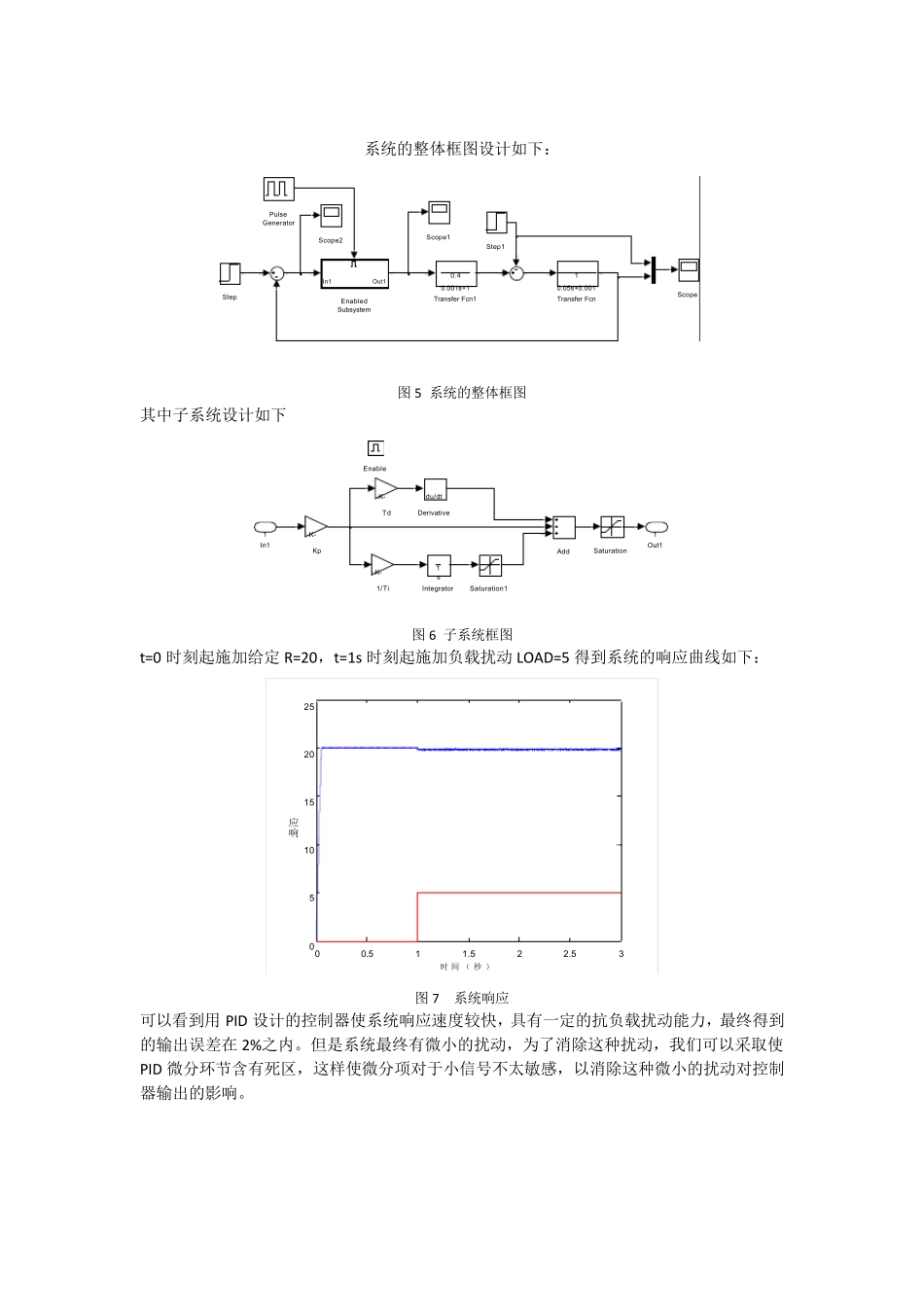
院系:控制系 姓名:刘锋 学号:M201071802 指导老师:关治洪 一、P ID 控制器的设计 1. PID 线性控制器至今在控制系统的应用中占有统治地位[3]。这是因为PID 控制器结构简单,使用方便,控制对象面广,在理论上有成熟的稳定性设计和参数整定方法,在工程应用中积累了丰富的实践经验。 PID 参数的整定方法很多,主要有Ziegler-Nichols 整定法,临界比例度法,衰减曲线法。 首先通过实验获取控制对象的单位阶跃响应,得到响应曲线如下: 00.511.522.5300.10.20.30.40.50.60.70.80.91时间 s被控对象的响应曲线 图1 单位阶跃响应曲线 可以看到单位阶跃响应曲线看起来不是一条S 形的曲线,所以不能用Ziegler-Nichols 方法来整定参数[1]。 考虑用临界比例度法,由于临界比例法要求系统的阶数是三阶或者三阶以上,所以不可以使用临界比例度法。 下面考虑衰减曲线法 用Simulink 搭建系统仿真图如下: 图2 断开积分微分后的阶跃响应 逐渐增大比例增益 K,观察示波器,直到响应系统的第一次超调量和第二次超调量之比为4:1时,记下此时的增益 K 值,可以得到K=290 时,比例度大约为4:1,此时比例度Ps=0.00345,Ts=0.0067s. 0.970.980.9911.011.021.031.041.051.0600.20.40.60.811.21.4时 间 ( 秒 ) k=290响应曲线 图 3 K=290 时系统的响应 有经验公式[2], 表 1 经验公式 计算得 Kp=362, Ti=0.002s, Td=0.00067s. 将子系统的参数按上述修改,得到仿真图如下: 图 4 t=1s 时,施加阶跃信号后的系统响应 可以看到 PID 控制能达到很好的控制效果。 系统的整体框图设计如下:0.40.001s+1Transfer Fcn110.05s+0.001Transfer FcnStep1StepScope2Scope1ScopePulseGeneratorIn1Out1EnabledSubsystem 图 5 系统的整体框图 其中子系统设计如下 1Out1-K-TdSaturation1Saturation-K-Kp1sIntegratordu/dtDerivativeAdd-K-1/TiEnable1In1 图 6 子系统框图 t=0 时刻起施加给定 R=20,t=1s 时刻起施加负载扰动 LOAD=5 得到系统的响应曲线如下: 00.511.522.530510152025时 间 ( 秒 )响应 图 7 系统响应 可以看到用 PID 设计的控制器使系统响应速度较快,具有一定的抗负载扰动能力,最终得到的输出误差在 2%之内。但是系统最终有微小的扰动,为了消除这种扰动,我们可以采取使PID 微分环节含有死区,这样使微分项对于小信号不太敏感,以消除这种微小的扰动对控制器输出的影响。...