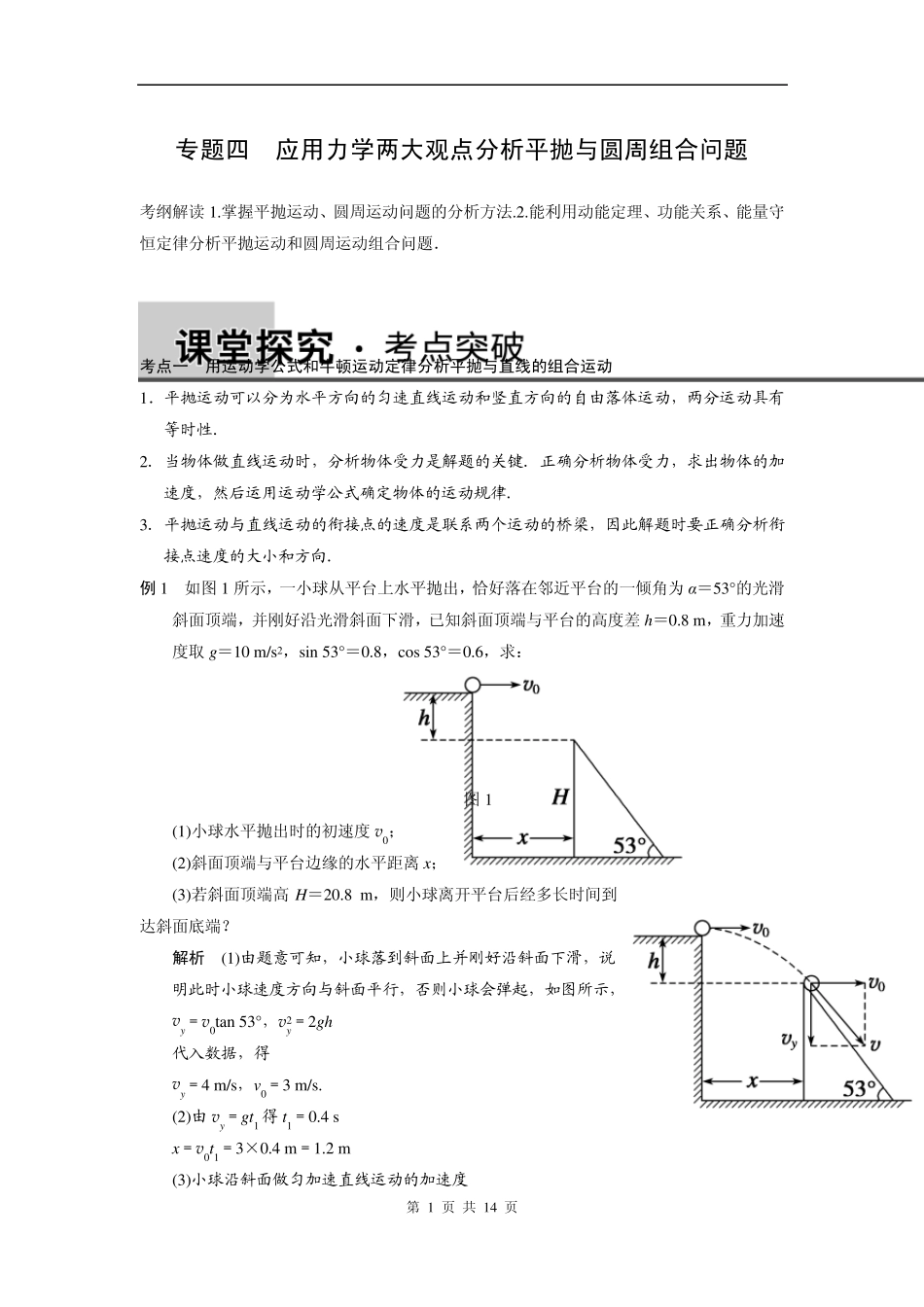
第 1 页 共 14 页 专题四 应用力学两大观点分析平抛与圆周组合问题 考纲解读1.掌握平抛运动、圆周运动问题的分析方法.2.能利用动能定理、功能关系、能量守恒定律分析平抛运动和圆周运动组合问题. 考点一 用运动学公式和牛顿运动定律分析平抛与直线的组合运动 1.平抛运动可以分为水平方向的匀速直线运动和竖直方向的自由落体运动,两分运动具有等时性. 2.当物体做直线运动时,分析物体受力是解题的关键.正确分析物体受力,求出物体的加速度,然后运用运动学公式确定物体的运动规律. 3.平抛运动与直线运动的衔接点的速度是联系两个运动的桥梁,因此解题时要正确分析衔接点速度的大小和方向. 例 1 如图1 所示,一小球从平台上水平抛出,恰好落在邻近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8 m,重力加速度取g=10 m/s2,sin 53°=0.8,cos 53°=0.6,求: 图1 (1)小球水平抛出时的初速度v0; (2)斜面顶端与平台边缘的水平距离x ; (3)若斜面顶端高H=20.8 m,则小球离开平台后经多长时间到达斜面底端? 解析 (1)由题意可知,小球落到斜面上并刚好沿斜面下滑,说 明此时小球速度方向与斜面平行,否则小球会弹起,如图所示, vy=v0tan 53°,v2y=2gh 代入数据,得 vy=4 m/s,v 0=3 m/s. (2)由vy=gt1 得 t1=0.4 s x =v0t1=3×0.4 m=1.2 m (3)小球沿斜面做匀加速直线运动的加速度 第 2 页 共 14 页 a=mgsin 53°m=8 m/s2 初速度v=v20+v2y=5 m/s Hsin 53°=vt2+12at22 代入数据,解得t2=2 s 或t2′=-134 s(不符合题意舍去) 所以 t=t1+t2=2.4 s. 答案 (1)3 m/s (2)1.2 m (3)2.4 s 考点二 用动力学和功能观点分析平抛与圆周的组合运动 1.物体的圆周运动主要是竖直面内的圆周运动,通常应用动能定理和牛顿第二定律进行分析,有的题目需要注意物体能否通过圆周的最高点. 2.平抛运动与圆周运动的衔接点的速度是解题的关键. 例 2 如图 2 所示,一粗糙斜面 AB 与圆心角为 37°的光滑圆弧 BC 相切,经过 C 点的切线方向水平.已知圆弧的半径为 R=1.25 m,斜面 AB 的长度为 L=1 m.质量为 m=1 kg 的小物块(可视为质点)在水平外力 F=1 N 作用下,从斜面顶端 A 点处由静止开始,沿斜面向下运动,当到达 B 点时撤去外力,物块沿圆弧滑至 C 点抛出,若落...