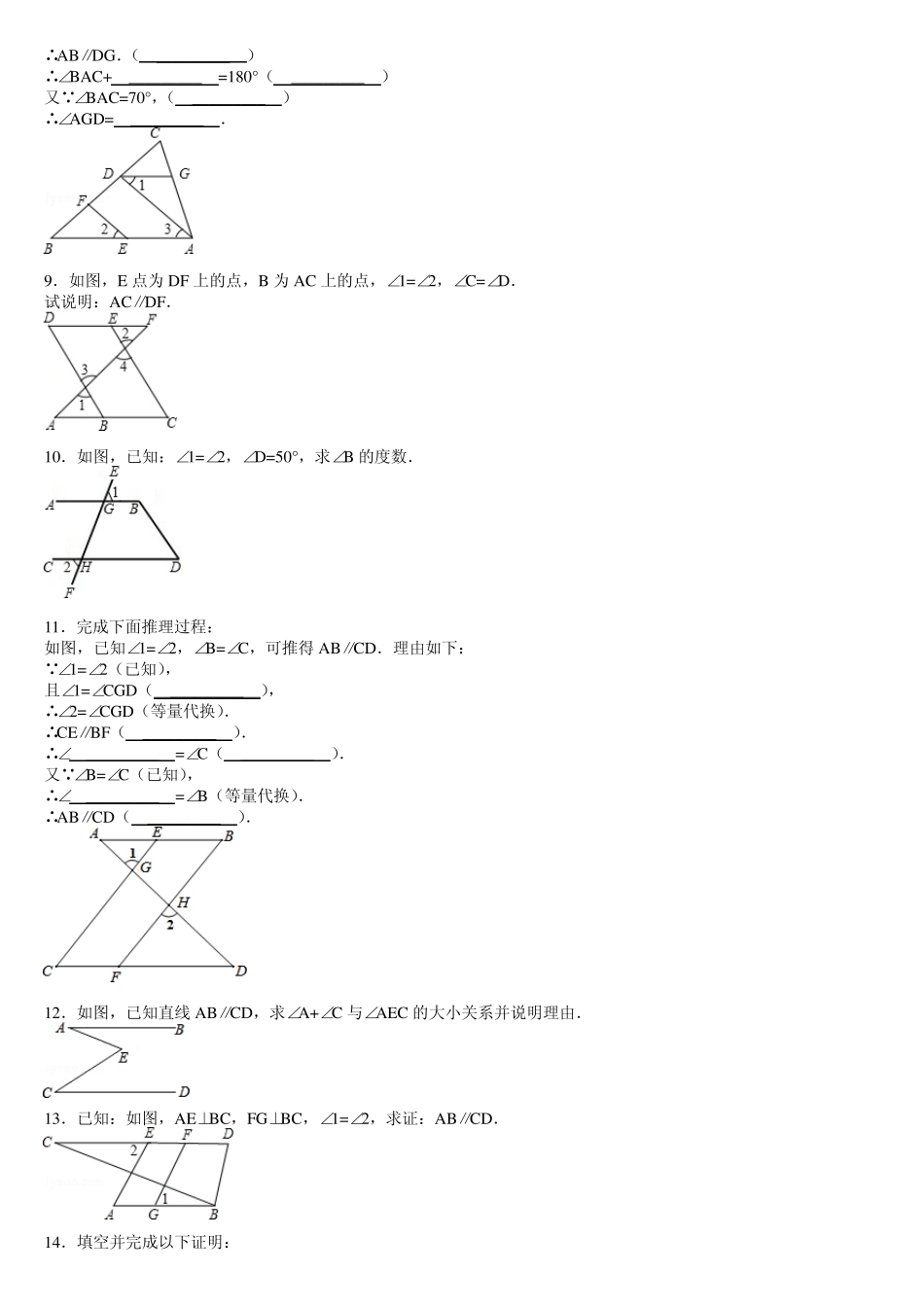
1.如图,直线AE、CF 分别被直线EF、AC 所截,已知,∠1=∠2,AB 平分∠EAC,CD 平分∠ACG.将下列证明 AB∥CD的过程及理由填写完整. 证明:因为∠1=∠2,所以 _________ ∥ _________ ,( _________ ) 所以∠EAC=∠ACG,( _________ ) 因为 AB 平分∠EAC,CD 平分∠ACG, 所以 _________ =, _________ =, 所以 _________ = _________ , 所以 AB∥CD( _________ ). 2.如图,∠1=∠2=∠3,完成说理过程并注明理由: 因为∠1=∠2(已知) 所以 _________ ∥ _________ ( _________ ) 因为∠1=∠3(已知) 所以 _________ ∥ _________ ( _________ ) 3.如图,已知AB∥CD,∠1=∠2,求证:BE∥CF. 4.如图,已知∠AED=60°,∠2=30°,EF 平分∠AED,可以判断 EF∥BD 吗?为什么? 5.如图,在四边形 ABCD 中,∠A=∠C,BE 平分∠ABC,DF 平分∠ADC,试说明 BE∥DF. 6.如图,AB∥CD,∠B=∠C,求证:AC∥BD. 7.(2011•淄博)如图,直线AB,CD 分别与直线AC 相交于点 A,C,与直线BD 相交于点 B,D.若∠1=∠2,∠3=75°,求∠4 的度数. 8.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD 的过程填写完整. EF∥AD,( _________ ) ∴∠2= _________ .(两直线平行,同位角相等;) 又 ∠1=∠2,( _________ ) ∴∠1=∠3.( _________ ) ∴AB∥DG.( _________ ) ∴∠BAC+ _________ =180°( _________ ) 又 ∠BAC=70°,( _________ ) ∴∠AGD= _________ . 9.如图,E 点为 DF 上的点,B 为 AC 上的点,∠1=∠2,∠C=∠D. 试说明:AC∥DF. 10.如图,已知:∠1=∠2,∠D=50°,求∠B 的度数. 11.完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得 AB∥CD.理由如下: ∠1=∠2(已知), 且∠1=∠CGD( _________ ), ∴∠2=∠CGD(等量代换). ∴CE∥BF( _________ ). ∴∠ _________ =∠C( _________ ). 又 ∠B=∠C(已知), ∴∠ _________ =∠B(等量代换). ∴AB∥CD( _________ ). 12.如图,已知直线 AB∥CD,求∠A+∠C 与∠AEC 的大小关系并说明理由. 13.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD. 14.填空并完成以下证明: 已知,如图,∠1=∠ACB,∠2=∠3,求证:∠BDC+∠DGF=180°. 证明: ∠1=∠ACB(...