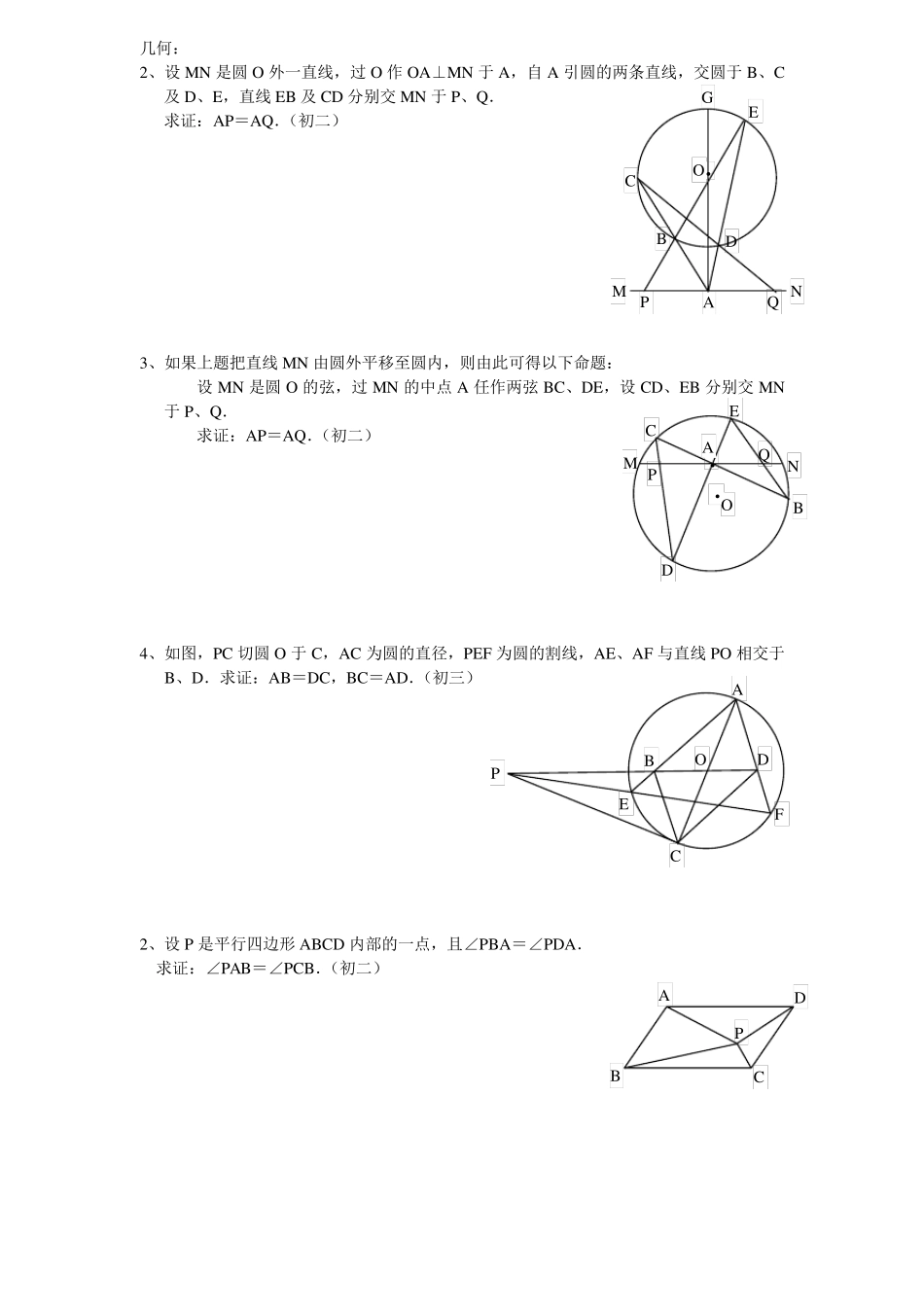
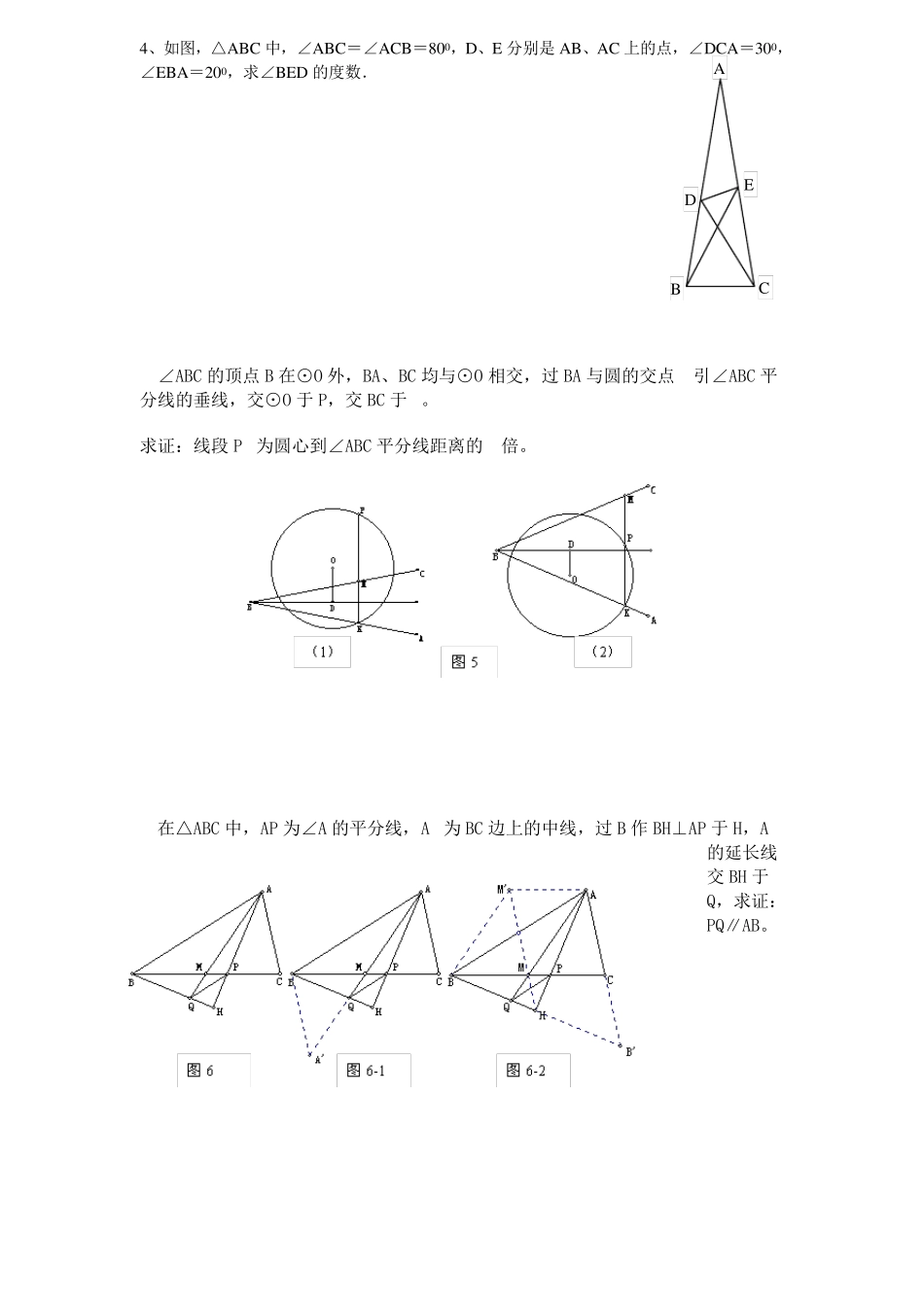
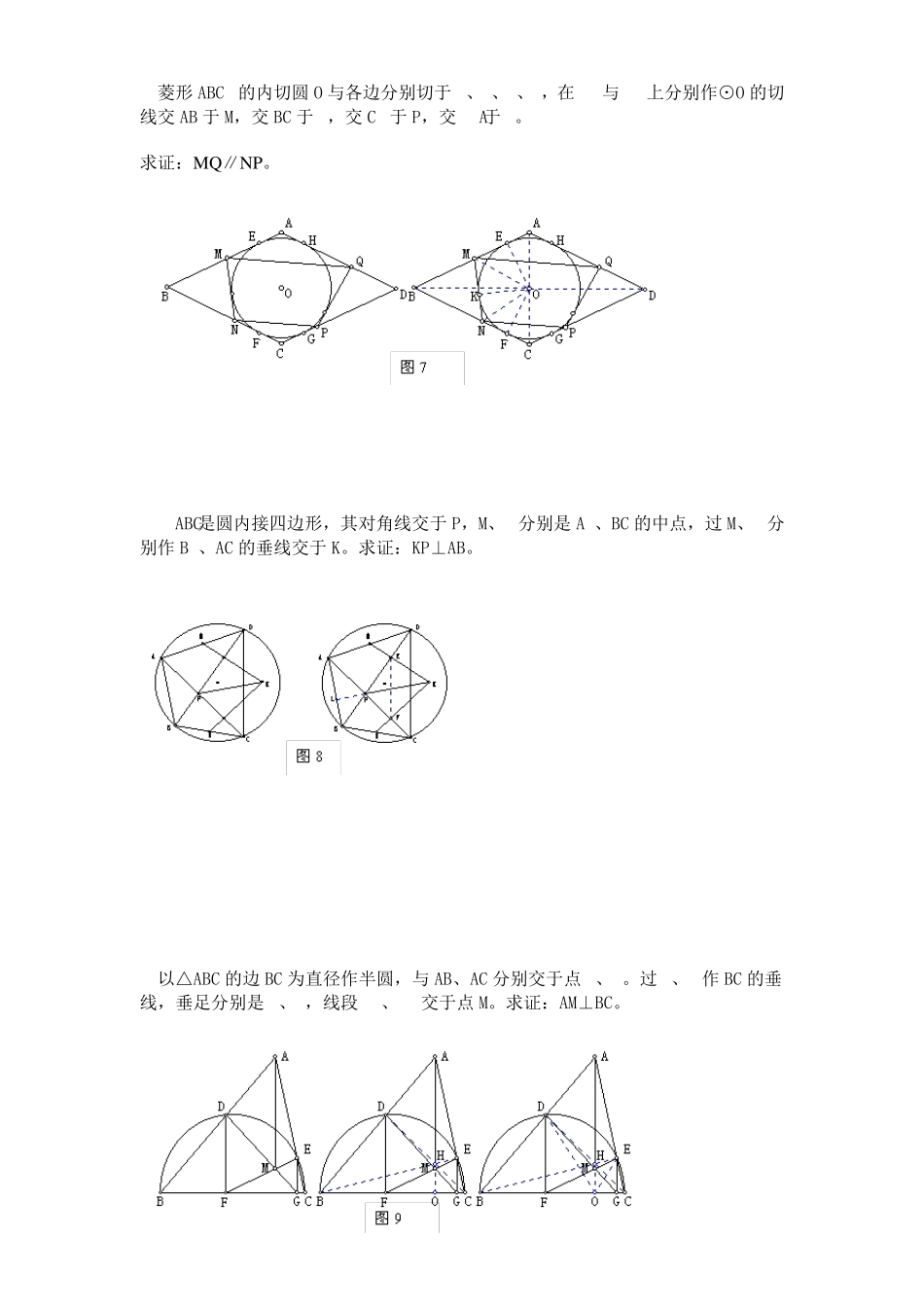
几何: 2、设MN 是圆O 外一直线,过O 作OA⊥MN 于A,自A 引圆的两条直线,交圆于B、C及D、E,直线EB 及CD 分别交MN 于P、Q . 求证:AP=AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC、DE,设CD、EB 分别交MN于P、Q . 求证:AP=AQ .(初二) 4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE、AF 与直线PO 相交于B、D.求证:AB=DC,BC=AD.(初三) 2、设P 是平行四边形ABCD 内部的一点,且∠PBA=∠PDA. 求证:∠PAB=∠PCB.(初二) · G A O D B E C Q P N M · O Q P B D E C N M · A O D B F A E C P P A D C B 4、如图,△ABC 中,∠ABC=∠ACB=800,D、E分别是 AB、AC 上的点,∠DCA=300,∠EBA=200,求∠BED 的度数. 1.∠ABC 的顶点 B 在⊙O 外,BA、BC 均与⊙O 相交,过 BA 与圆的交点 K引∠ABC 平分线的垂线,交⊙O 于 P,交 BC 于 M。 求证:线段 PM为圆心到∠ABC 平分线距离的 2倍。 2.在△ABC 中,AP 为∠A 的平分线,AM为 BC 边上的中线,过 B 作 BH⊥AP 于 H,AM的延长线交 BH 于Q,求证:PQ∥AB。 E D C B A 3.菱形ABCD的内切圆O 与各边分别切于E、F、G、H,在EF与GH上分别作⊙O 的切线交AB 于M,交BC 于N,交CD于P,交DA于Q。 求证:MQ ∥NP。 4.ABCD是圆内接四边形,其对角线交于P,M、N分别是 AD、BC 的中点,过 M、N分别作BD、AC 的垂线交于K。求证:KP⊥AB。 5.以△ABC 的边BC 为直径作半圆,与AB、AC 分别交于点 D、E。过 D、E作BC 的垂线,垂足分别是 F、G,线段 DG、EF交于点 M。求证:AM⊥BC。 6.△ABC 内接于⊙O,P是弧 AB上的一点,过P作OA、OB 的垂线,与AC、BC 分别交于S、T,AB 交于M、N。求证:PM=MS充要条件是PN=NT。 7.已知A 为平面上两半径不等的圆O1和O2的一个交点,两外公切线P1P2、Q1Q2分别切两圆于P1、P2、Q1、Q2,M1、M2分别为P1Q1、P2Q2的中点。求证:∠O1AO2=∠M1AM2。 5.如图,已知∠BAC=90º,AD⊥ BC, ∠1=∠2,EF⊥ BC, FM⊥ AC,说 明 FM=FD的理 由 6.如图,已知△ABD 和△ACE 是直 角 三 角 形 ,∠ABD=∠ACE=90°,∠BAD=∠CAE,连 接DE,点M 为DE 边 中点,求证:BM =CM 。 7.如图,已知△ABC 和△ADE 都是等腰直角...