相似三角形综合题

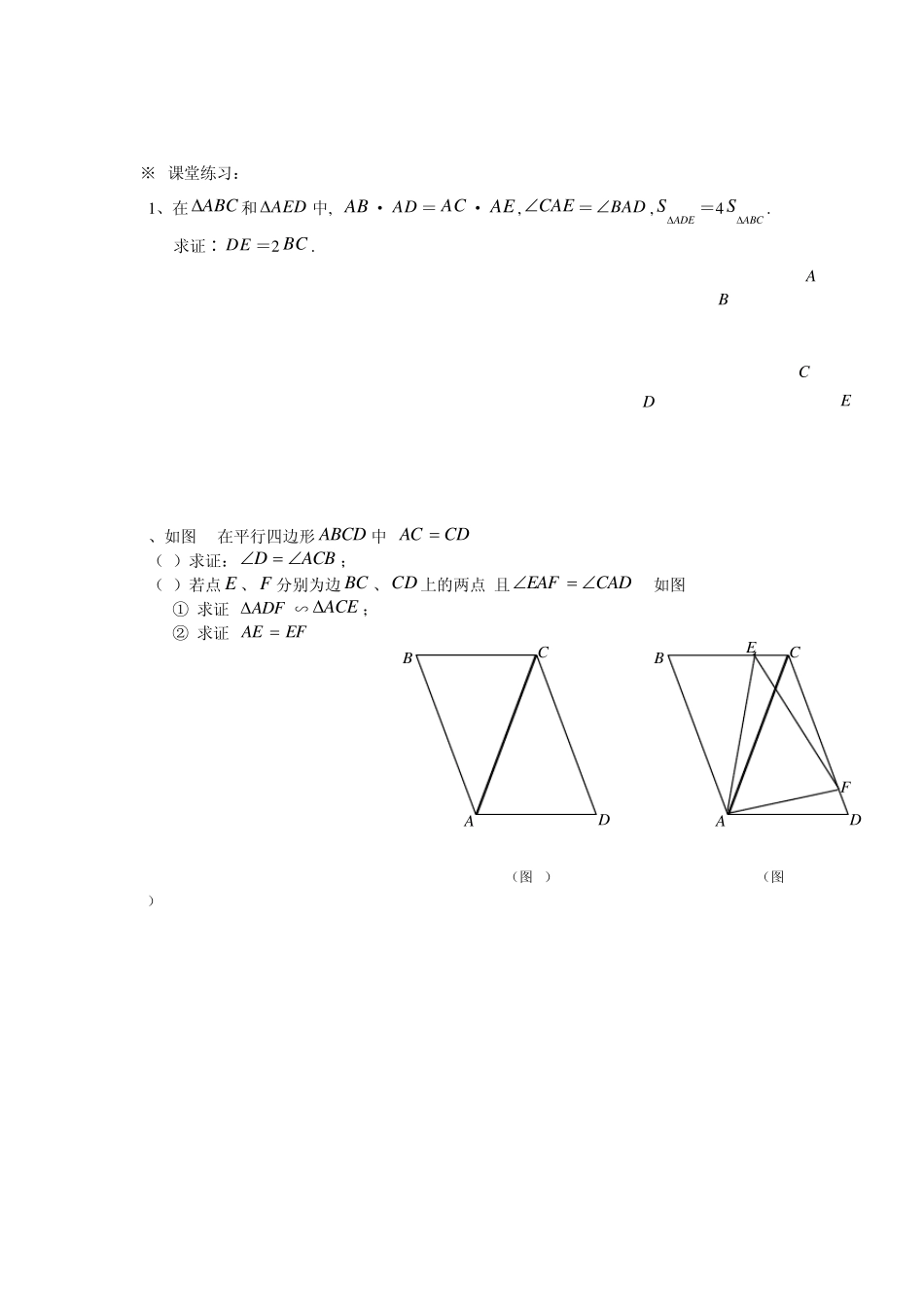
相似三角形综合题精选 1、在Rt ABC中, ∠ACB=90°, CDAB,垂足为 D . E 、F 分别是 AC 、BC 边上一点, 且CE=13 AC , BF =13 BC . (1 )求证∶ ACBC =CDBD . (2 )求EDF的度数. 2、在矩形ABCD 中，AB=4，AD=5，P 是射线 BC 上的一个动点，作 PE⊥AP，PE 交射线DC 于点 E，射线 AE 交射线 BC 于点 F，设 BP=x ，CE=y ． （1）如图，当点 P 在边 BC 上时（点 P 与点 B、C 都不重合），求 y 关于 x 的函数解析式，并写出它的定义域； （2）当 x =3 时，求 CF 的长； （3）当 EP/AP= 21 时，求 BP 的长． A B P C F D E FEDCBA 3 、（1 ）在ABC中，5 ACAB，8BC，点P 、Q 分别在射线CB 、AC 上（点P 不与点C 、点B 重合），且保持ABCAPQ. ①若点P 在线段CB 上（如图），且6BP，求线段CQ 的长； ②若xBP ，yCQ ，求 y与x之间的函数关系式，并写出函数的定义域； （2 ）正方形 ABCD 的边长为5 （如图 2 ），点P 、Q 分别在直线．．CB 、DC 上（点P 不与点C 、点B 重合），且保持9 0APQ.当1CQ时，写出线段 BP 的长 （不需要计算过程，请直接写出结果）. 图 1 A B C 备用图 A B C P Q A B C D 图 2 F E D C B A D C B A ※ 课堂练习： 1 、在ABC和AED中, AB · AD ＝ AC · AE ,CAE＝BAD,ADES＝4ABCS. 求证∶ DE ＝2 BC . 2、如图 1,在平行四边形 ABCD 中,CDAC . （1）求证：ACBD； （2）若点 E 、F 分别为边 BC 、CD 上的两点,且CADEAF.(如图 2) ① 求证: ADF∽ ACE； ② 求证:EFAE . （图 1） （图2） EDCBA 3、如图，在梯形ABCD 中，AB ∥CD ，90A，2AB，3BC,1CD， E是AD 的中点. （1）求证：CDE∽EAB； （2）CDE与CEB有可能相似吗？若相似，请给出证明过程；若不相似，请简述理由. 4、已知：如图，在△ABC 中，∠ADE = ∠B，∠BAC = ∠DAE． （1）求证：ACAEABAD ； （2）当∠BAC = 90°时，求证：EC⊥BC． A B C E D A B C D E 5、如图，矩形EFGD 的边EF 在ABC的BC 边上，顶点D 、G 分别在边AB 、AC 上． 已知5ABAC，6BC ，设BEx，EFGDSy矩形． （1）求y 关于x的函数解析式，并写出自变量x的取值范围； （2）...