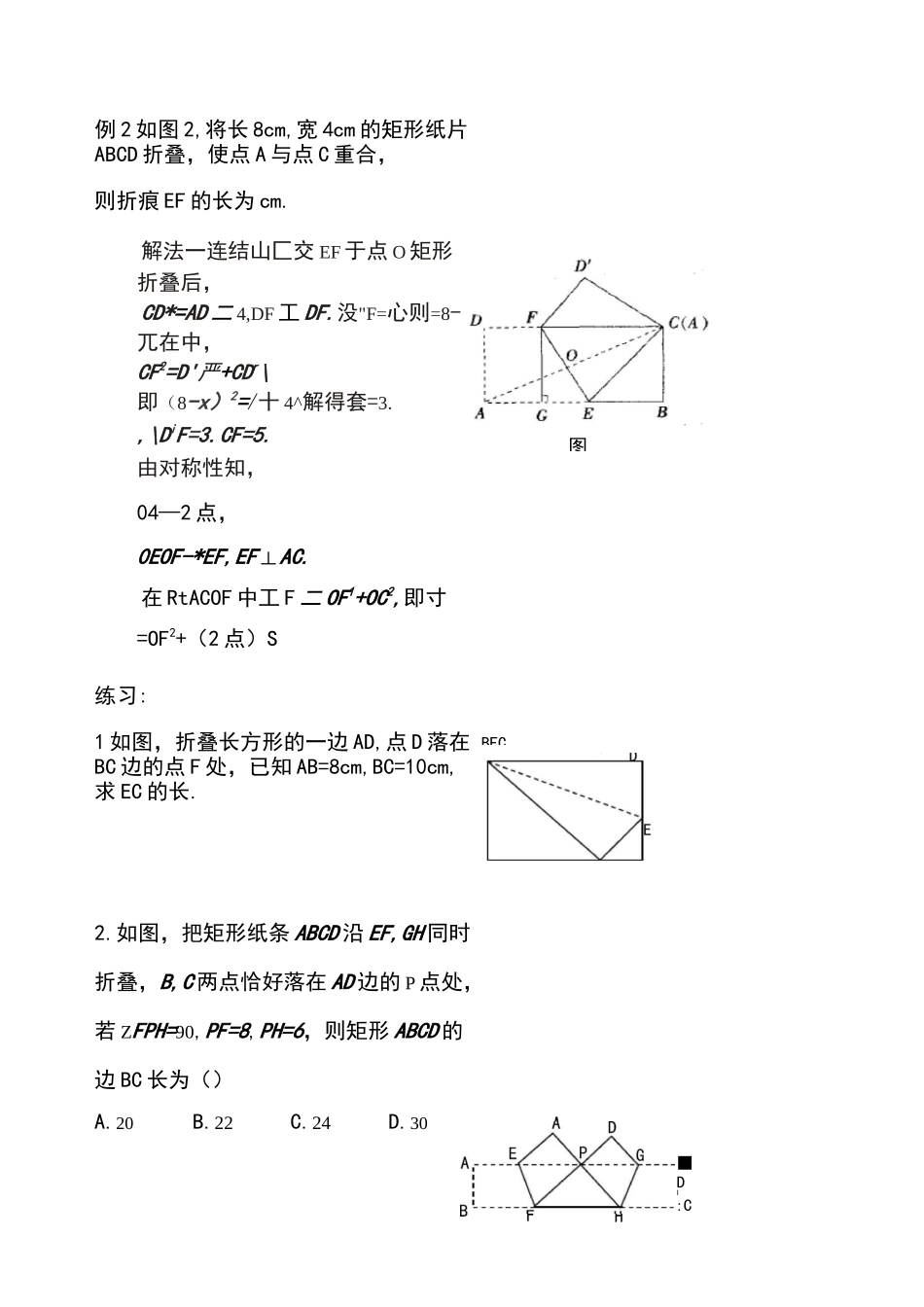
武汉龙文教育学科辅导教案学生教师学科时间星期时间段一、翻折问题例 1 在平面直角坐标系中,已知两点,点 C(o,n)是 y 轴 上一点直线 y=—3x+34•把坐标平面沿直线 AC 折叠,使点 B 刚好落与 x 轴、y 轴分别交于 A、B在 x 轴上,则点 C 的坐标).(0,3)(B)4解析设折叠后点”刚好幫在玄軸上点 D 朴如图 1 所示.由对称性知=AD.BC=CD在 RtATiOfi 中 fAB::73^+z.AD=AB=5,OD 已 知 OC=4 则 CD 在RtiCOD 中,CD,(A:(0,43)(C)(0,=BC=3-7L=OC"3)练习:轴、y(D)(0,u(/|4)即(3-*-如图,把矩形纸片轴上,连结 AC,将若点 E 的坐标为(1,2),解得0 环选丘OABC 放入平面直角坐标系中,使 OA、0C 分别落在 x矩形纸则点 D片 OABC 沿 AC 折叠,使点 B 落在点 D 的位置,的横坐标是.图3例 2 如图 2,将长 8cm,宽 4cm 的矩形纸片ABCD 折叠,使点 A 与点 C 重合,则折痕 EF 的长为 cm.解法一连结山匚交 EF 于点 O 矩形折叠后,CD*=AD 二 4,DF 工 DF.没"F=心则=8-兀在中,CF2=D'严+CDr\即(8-x)2=/十 4^解得套=3.,\DiF=3.CF=5.由对称性知,04—2 点,0EOF-*EF,EF 丄AC.在 RtACOF 中工 F 二 OF1+OC2,即寸=OF2+(2 点)S练习:1 如图,折叠长方形的一边 AD,点 D 落在BC 边的点 F 处,已知 AB=8cm,BC=10cm,求 EC 的长.2.如图,把矩形纸条 ABCD 沿 EF,GH 同时折叠,B,C 两点恰好落在 AD 边的 P 点处,若 ZFPH=90,PF=8,PH=6,则矩形 ABCD 的边 BC 长为()图BFCA.20B.22C.24D.30■DI:C25二子心=7例 3 如图 4,有一张矩形纸片 ABCD,其中 AD=8cm,AB=6cm,将矩形纸片先沿对角线 BD 对折,点 C 落在点 C'的位置,BC'交 AD 于点 G.(1)求证:AG=C'G;⑵ 如图 5,再折叠一次,使点 D 与点 A 重合,得折痕 EN,EN 交 AD 于点 M,求 EM 的长.解析(1)法一由对称性,集CrD=CD==9牛厶网=^AGB=厶 G'GLAB-CDCD,/.ZU 我&竺^CrDG,二 AG-C'G.法二由对称性■知图 4BCf=RC,乙 GRD=LDBC.「AD//BC.几 AGDB 七厶 DRG,二^LGBD=2LGDB,+\GD=GBr乂-AD 二陀…+AG=CG.(2)设 DG—x,则 CfG=AG=S-x.在 RtAGUD 中,GO*=C 点+C 即/二(8—工)工+6°,解得 x—才+打^DME5Z^DCG,EM4即号 1=才解得册T练习:1.如图,将矩形纸片 ABCD 沿对角线 BD 折叠,点 C 落在点 E 处,BE 交 AD于点 F,连结 AE■证明:⑴ BF=DF-⑵AE〃BD-⑶ 若 AB=6,BC=10,分别求 AF...