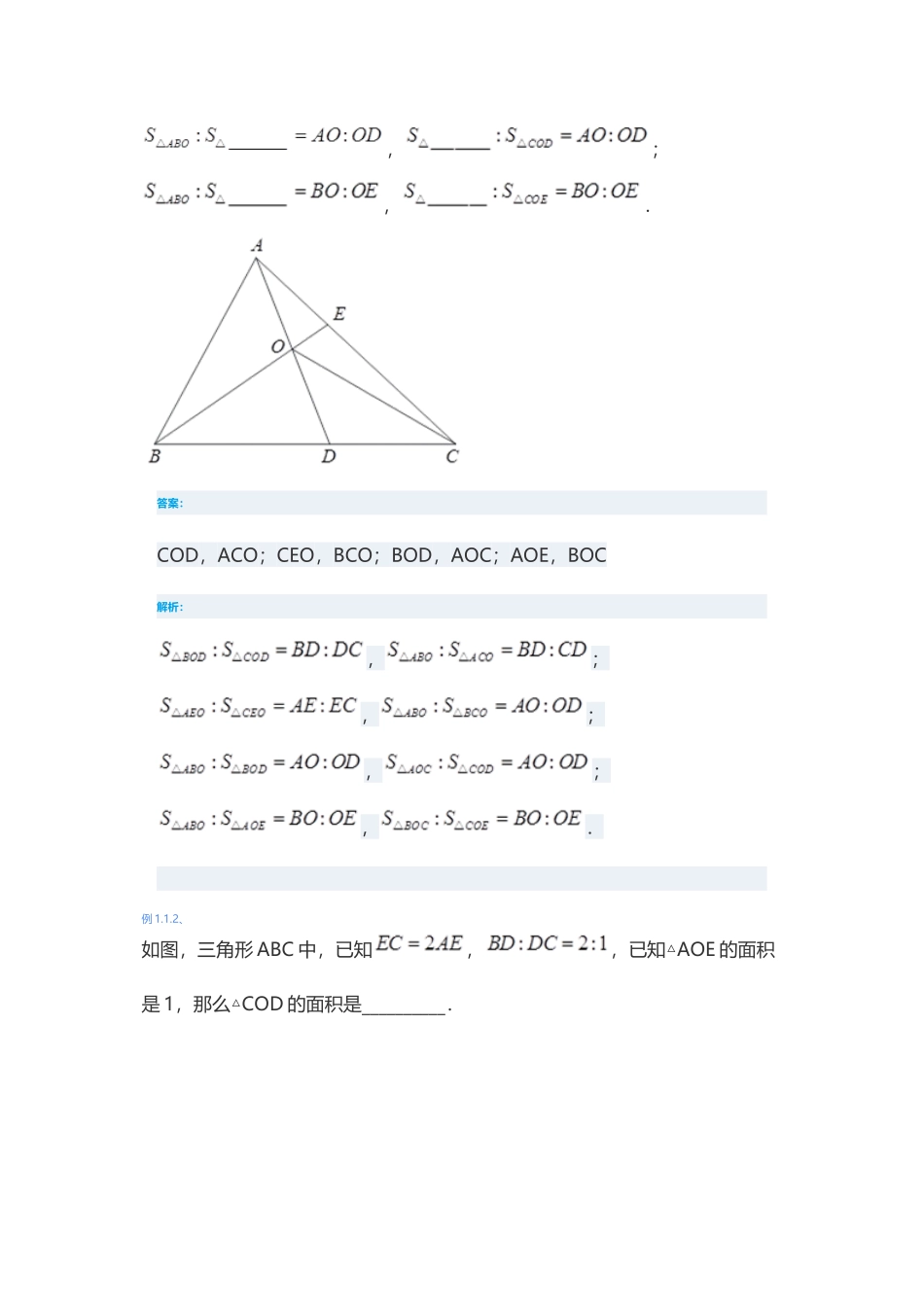
几何第 04 讲_基础燕尾模型知识图谱几何第 04 讲_基础燕尾模型-一、基础燕尾模型已知两外比的应用已知一外比一内比的应用已知两内比的应用一:基础燕尾模型知识精讲根据等高三角形中的比例关系,我们可以得到如图所示的结论.我们把这种图形,称为燕尾模型.三点剖析重难点:如何选择合适的份数,使得份数统一.常用的方法:①最小图形面积为中心,进行标份数;②公共部分的整数化,优先考虑.通常已知两内比的燕尾模型,需要借助未知数解决问题.题模精讲题模一 已知两外比的应用例 1.1.1、根据图中的比例关系填空.,;,;,;,.答案:COD,ACO;CEO,BCO;BOD,AOC;AOE,BOC解析:,;,;,;,. 例 1.1.2、如图,三角形 ABC 中,已知,,已知△AOE 的面积是 1,那么△COD 的面积是__________.答案:4解析:标数如图所示.所以那么△COD 的面积是 4. 例 1.1.3、在△ABC 中,,,OB 的长度是 OE 的__________倍.答案:2解析:标份数如图所示.所以,即 OB 的长度是 OE 的 2 倍. 例 1.1.4、如图,在三角形 ABC 中,,,已知三角形 ABC 面积是1,那么三角形 ABO 的面积是_______.答案:解析:连结 OC,设面积为 1 份,则面积也为 1 份.根据燕尾模型,,故面积为 4 份.这样,. 例 1.1.5、如图,的三边上各有一点 D、E、F,三条线段 AD、BE、CF 相交于同一点 O.已知、的面积分别是 65 和 16,.求的面积.答案:20解析:,且,故,,进而,,.因此. 例 1.1.6、如图,已知正方形 ABCD 中,F 是 BC 边的中点,GC=2DG,E 是 DF 与 BG 的交点.四边形 ABED 的面积与正方形 ABCD 的比是______.答案:5:8解析:如图连接 BD 和 CE,设 DGE 的面积为 1 份,则 CGD 的面积为 2,DEB 的面积为 2,BGD 的面积为 4,BCG 的面积为 8,长方形的面积为 24,四边形 ADEB 的面积为 15,. 例 1.1.7、如图,在四边形 ABCD 中,,,四边形 AEOf 的面积是12,BCDE 的是平行四边形.那么四边形 ABCD 的面积是多少?答案:56解析:连接 BD 和 AO,利用燕尾模型中的比例关系,可以标出△ABD 中每一块的份数.因为 BCDE 是平行四边形,可知△BCD 的面积也是 7 份.,四边形 ABCD 的面积是 56. 题模二 已知一外比一内比的应用例 1.2.1、在 rABC 中,,F 是 AD 的中点,rABC 的面积是 12,则阴影部分的面积是__________.答案:7解...