立体几何的截面问题选题

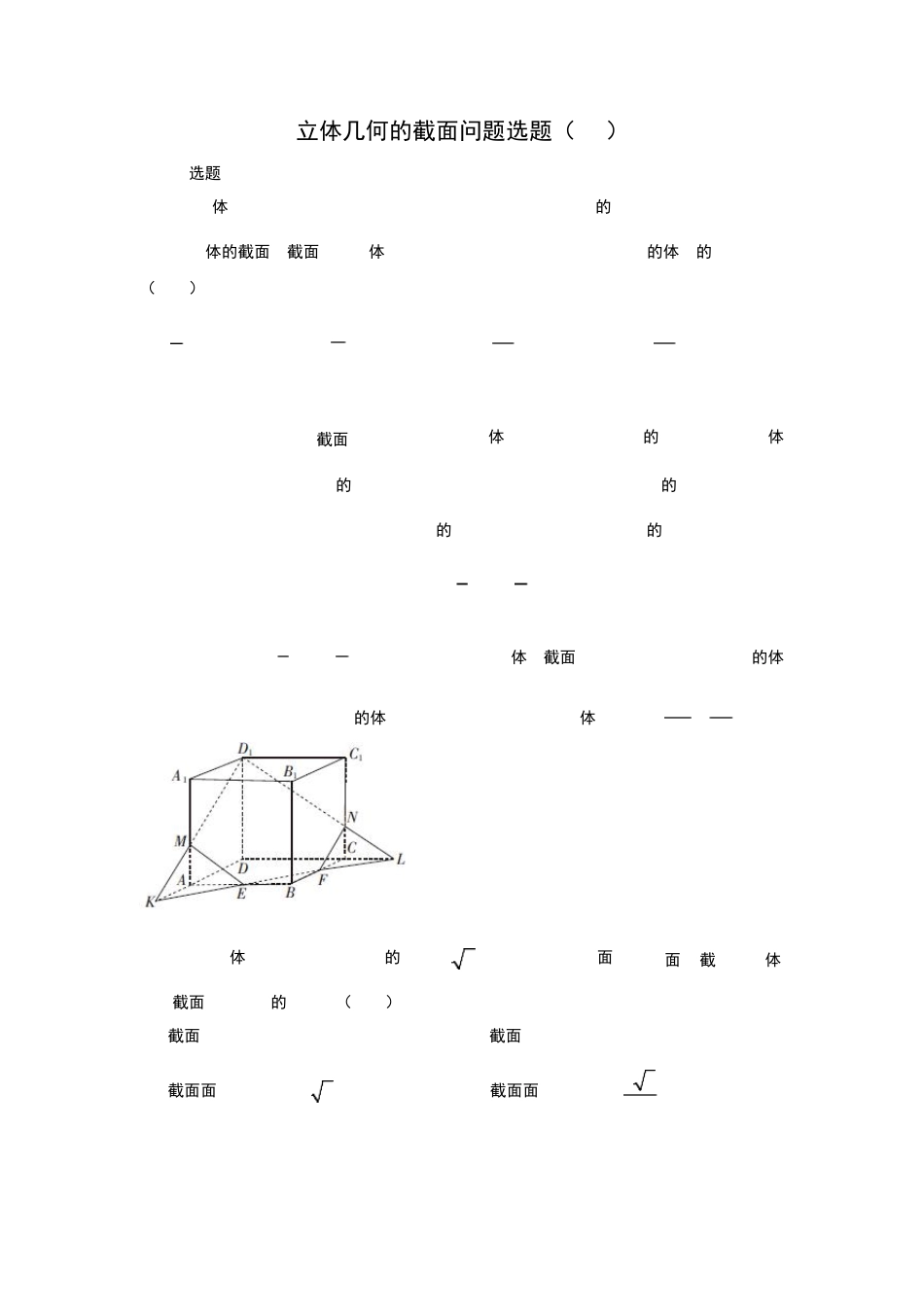
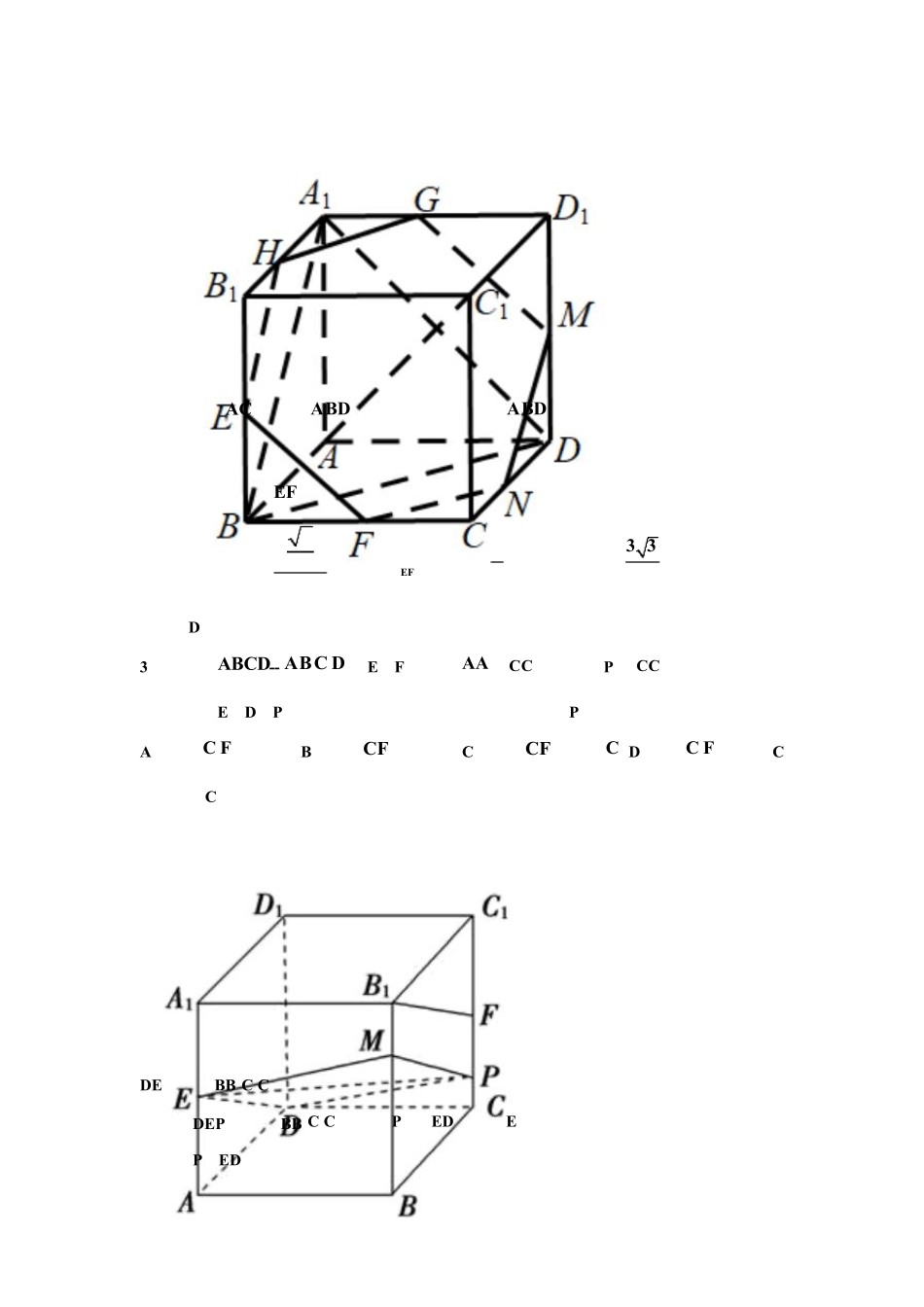
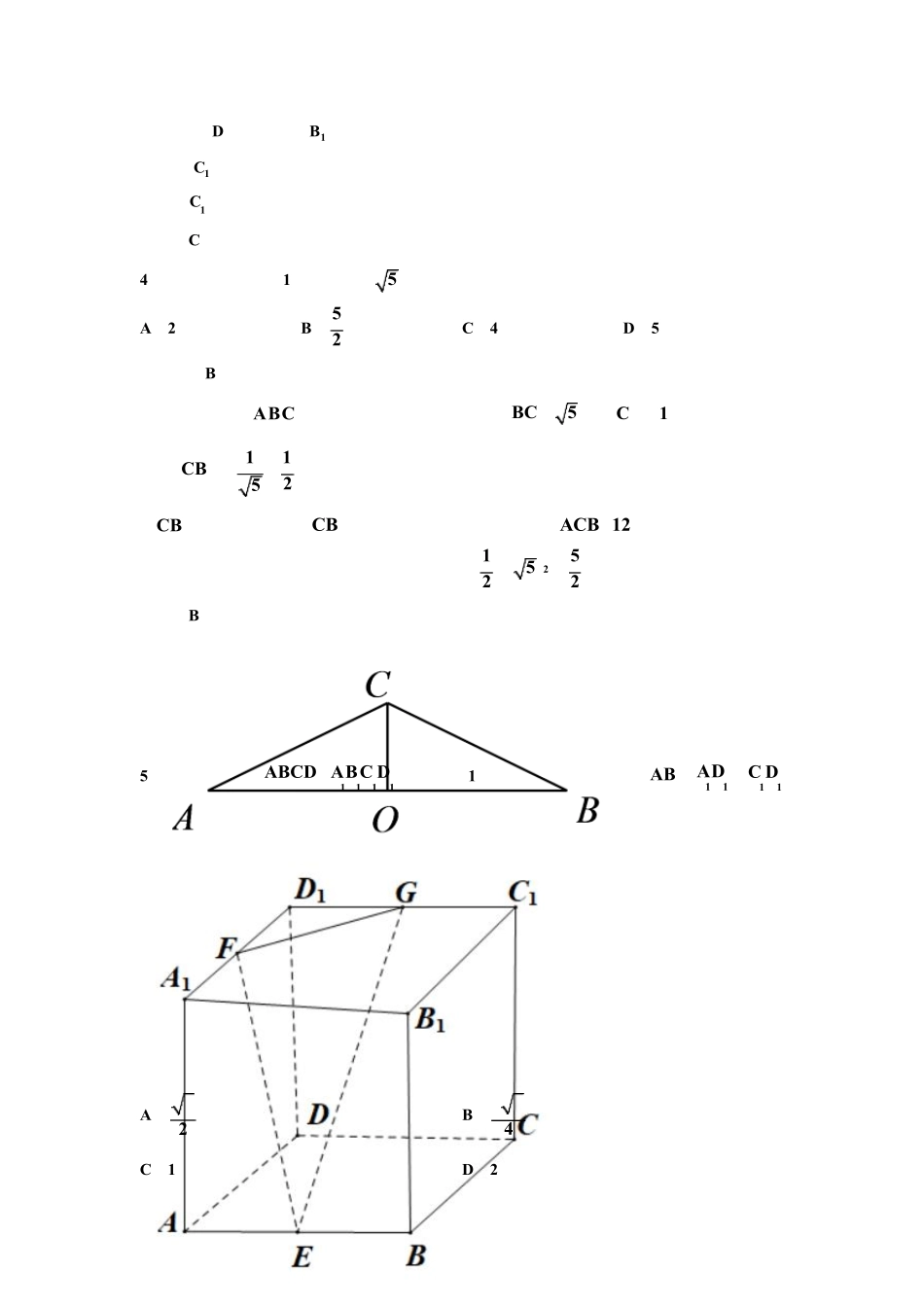
立体几何的截面问题选题（9.5）一、单选题1．在正方体1 1 1 1ABCDABCD中，E，F分别为棱 AB，BC的中点，过点1D，E，F作该正方体的截面，截面将正方体分成两部分，则较小部分与较大部分的体积的比值为（）A． 14B． 12C． 2349D． 2547【答案】D【详解】如图，可以作出截面1DMEFN，设正方体1 1 1 1ABCDABCD的棱长为 6，则其体积为 216，延长1DM 交 DA的延长线于点 K，连接 KE，延长1DN交 DC的延长线于点 L，连接 FL.因为 E， F分别为棱 AB， BC的中点， M ， N分别为两棱的三等分点，所以3AK CL ，2AM CN ，11169 98132D DKLV   ，1123 3332M AKEN CFLVV   ，所以正方体被截面分成两部分，其中一部分的体积为816 75 ，另外一部分的体积为 21675141，所以体积比值为75 2514147.2．已知正方体1 1 1 1ABCDABCD的棱长为2，直线1AC平面，平面截此正方体所得截面中，正确的说法是（）A．截面形状可能为四边形B．截面形状可能为五边形C．截面面积最大值为 2 3D．截面面积最大值为 332【答案】D【详解】如图在正方体中1AC 平面1ABD ，所以平面与平面1ABD 平行平面与正方体的截面可以是三角形、六边形但不会是五边形和四边形当截面为正六边形 EFNMGH时，截面面积有最大，由题可知：221sin45NM，则13 3611 sin6022  EFNMGHS故选：D3．正方体 ABCD--1111DCBA，E、F 分别是1AA、1CC 的中点，P 是1CC 上的动点（包括端点），过 E、D、P 作正方体的截面，若截面为四边形，则 P 的轨迹是A．线段1C FB．线段CFC．线段CF 和一点1C D．线段1C F 和一点 C．【答案】C【详解】如图所示，DE∥平面 BB1C1C，∴平面 DEP与平面 BB1C1C 的交线 PM∥ED，连接 EM，易证 MP=ED，∴MP∥ED，则 M到达 B1 时仍可构成四边形，即 P到 F．而 P在 C1F之间，不满足要求．P到点 C1 仍可构成四边形．故选：C．4．已知圆锥的高为 1，母线长为5 ，则过此圆锥顶点的截面面积的最大值为（）A．2B． 52C．4D．5【答案】B【详解】如图ABC是圆锥的轴截面，由题意母线5BC ，高1CO ，则11sin25CBO ，CBO是锐角，所以30CBO ，于是得轴截面顶角12090ACB ，所以当两条母线夹角为90时，截面面积为215(5)22S  为所求面积最大值．故选：B...