第2章：一元线性回归方法

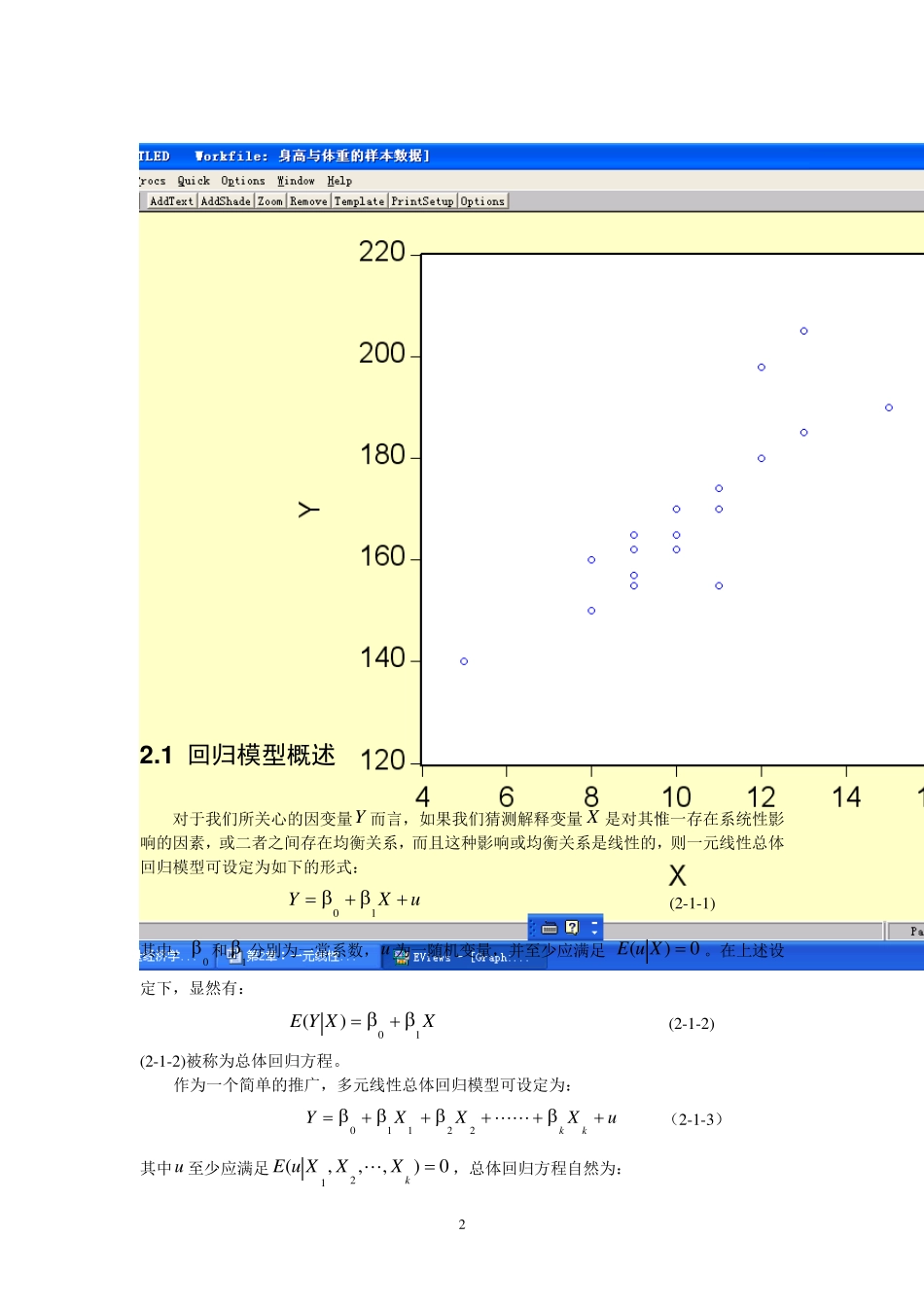
1 第2 章：一元线性回归方法 2 .0 问题导入 在前述游乐场猜体重的事例中，经营者获得了一个身高与体重的样本观察数据（见表2 -0 ），你如何利用这个观测数据集合来改善你的经营业绩呢？ 表 2 -0 身高与体重的样本观察数据 身高超过5 英尺以上的ix （单位：英寸） 体重（单位：磅） 5 9 1 3 1 2 1 0 1 1 8 9 1 0 1 2 1 1 9 1 0 1 2 8 9 1 0 1 5 1 3 1 1 1 4 0 1 5 7 2 0 5 1 9 8 1 6 2 1 7 4 1 5 0 1 6 5 1 7 0 1 8 0 1 7 0 1 6 2 1 6 5 1 8 0 1 6 0 1 5 5 1 6 5 1 9 0 1 8 5 1 5 5 2 2 .1 回归模型概述 对于我们所关心的因变量Y 而言，如果我们猜测解释变量X 是对其惟一存在系统性影响的因素，或二者之间存在均衡关系，而且这种影响或均衡关系是线性的，则一元线性总体回归模型可设定为如下的形式： uXY10 (2 -1 -1 ) 其中，0 和1 分别为一常系数，u 为一随机变量，并至少应满足 0)(XuE。在上述设定下，显然有： XXYE10)(  (2 -1 -2 ) (2 -1 -2 )被称为总体回归方程。 作为一个简单的推广，多元线性总体回归模型可设定为： uXXXYkk22110 （2 -1 -3 ） 其中u 至少应满足0),,,(21kXXXuE，总体回归方程自然为： 3 kkkXXXXXXYE2211021),,,( （2-1-4） 接下来，我们希望通过获得因变量和解释变量的一个容量为 n 的样本观测数据集niXYii,,2,1:),(，来对模型(2-1-1)中的参数0 和1 做出正确的估计。在多元情形中 ， 样 本 数 据 集 表 示 为 ： niXXXYikiii,,2,1:),,,,(21， 待 估 计 参 数 为 ：k,,,10。我们如何找到这样一种估计方法呢？ 假定我们找到了一种估计方法（正确与否暂时还无法判断），利用样本数据，我们对模型（2-1-1）参数0 和1 给出的估计量（值）为0ˆ 和1ˆ 。显然，0 和1 不能通过简单地将niXYii,,2,1:),(代入(2-1-1)而解出。但与(2-1-1)相对应，我们可以建立相应的样本回归模型： niuXYiii,,2,1ˆˆˆ10 (2-1-5) 其中，0ˆ 和1ˆ 是（假定）根据样本数据求出的对0 和1 的估计值，而iuˆ 则称为样本回归模型的残差或剩余，它可以被理解为利用样本数据对iu 的可能取值的一种估计...