第7章尺度检验(非参数统计,西南财大)

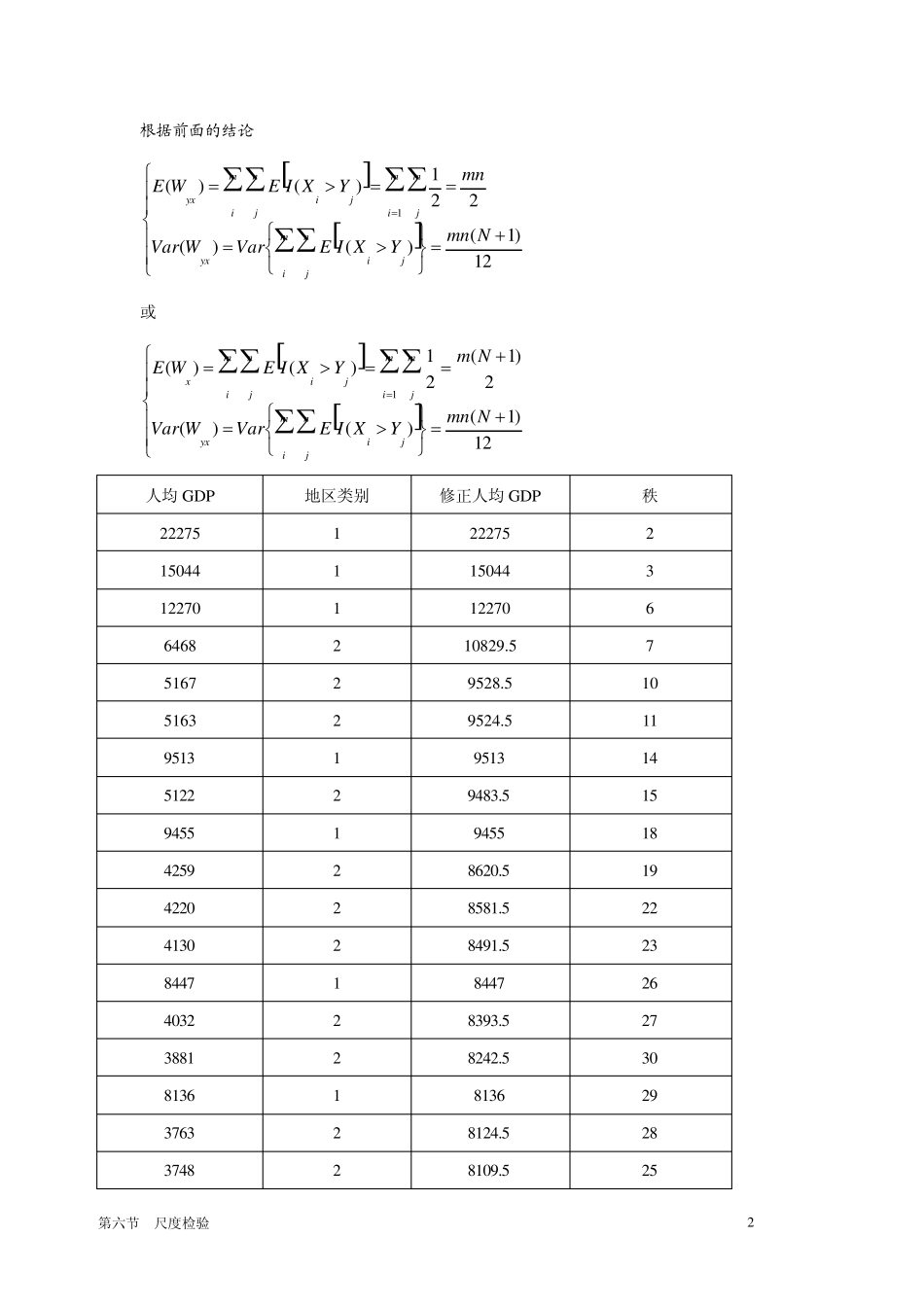
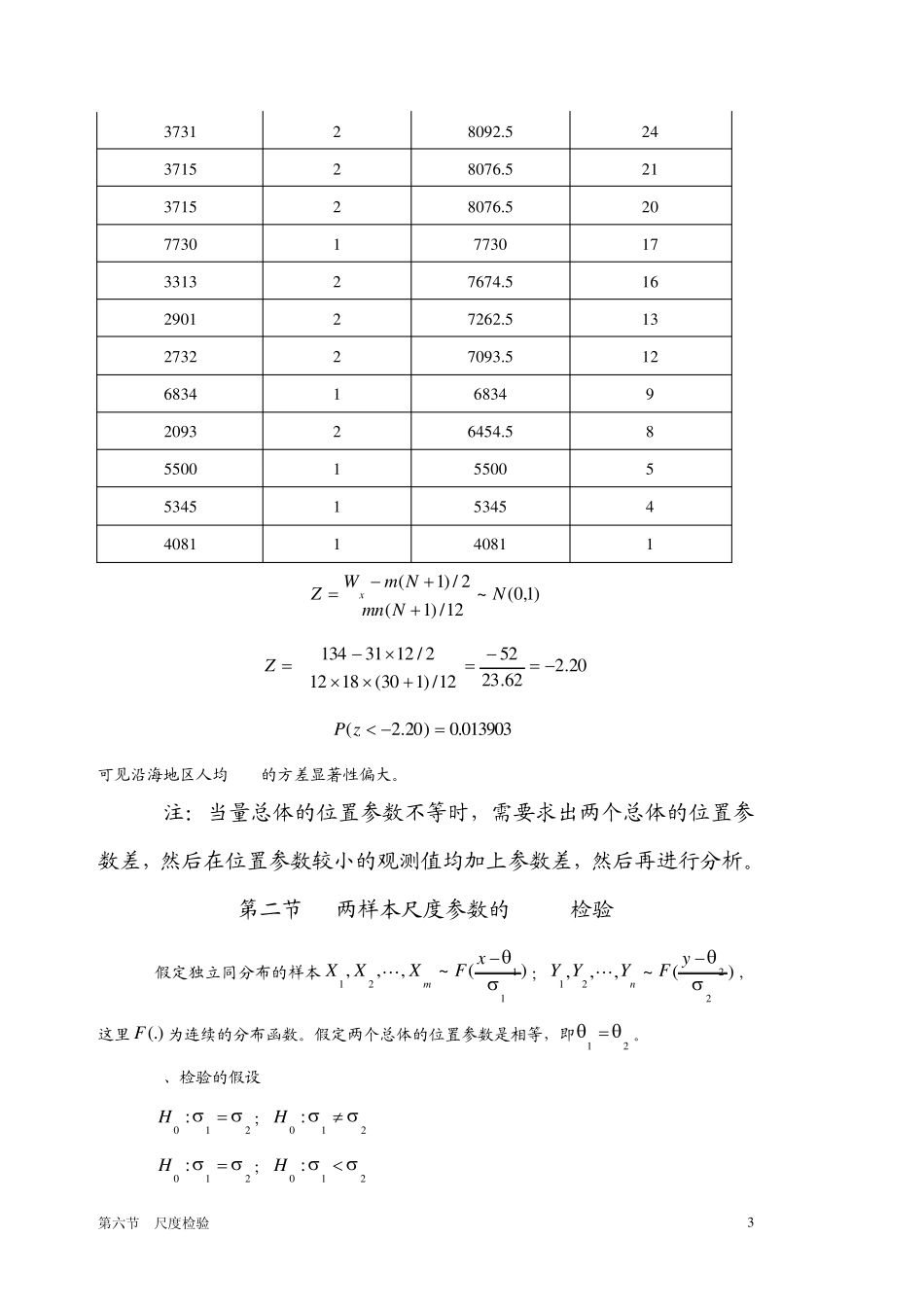
第六节 尺度检验 1 第七章 尺度检验 描述总体分布分散程度的参数为尺度参数（scale parameter）在初等的数理统计终，为了检验总体分散程度的指标是方差。对两个总体的方差进行检验，通常用F检验，统计量为： njjmiinyymxxF12121/()()1/()( 在原假设成立的条件下，该统计量服从F分布。但当总体不是正态分布时，则该种方法是不行的。以下的检验全部都是在模型的形状相同，位置参数相等的假定下。 第一节 两独立样本的Siegel-Tukey方差检验 假定有两独立样本 )(~,,,1121xFXXXm 和)(~,,,2221xFYYYn。 这里假定F(.)为连续函数，而且以Y轴为对称，且21 。 检验的假设： :0H样本来自同一总体分布 :1H样本来自同一总体分布仅仅方差不同。 顺序统计 量 )1(X )2(X )3(X ┅ )3( nX )2( nX )1( nX )(nX 秩 1 4 5 ┅ 7 6 3 2 如果一个总体方差比较大，那么它的最大值和最小值之间的差异会比较大。如果两个总体的标志变动度的比较，两个总体的样本混合排序以后，分散程度大的总体的样本可能会排在首尾，可能的秩和较小，而分散程度教小的可能排在中位数左右，所以 2)1( nnWWyxy 或2)1( nnWWyxy 2)1(mmWWxyx或2)1(mmWWxyx 第六节 尺度检验 2 根据前面的结论    12)1()()(221)()(1NmnYXIEVarWVarmnYXIEWEminjjiyxmimjminjjiyx 或    12)1()()(2)1(21)()(1NmnYXIEVarWVarNmYXIEWEminjjiyxmimjminjjix 人均 GDP 地区类别 修正人均 GDP 秩 22275 1 22275 2 15044 1 15044 3 12270 1 12270 6 6468 2 10829.5 7 5167 2 9528.5 10 5163 2 9524.5 11 9513 1 9513 14 5122 2 9483.5 15 9455 1 9455 18 4259 2 8620.5 19 4220 2 8581.5 22 4130 2 8491.5 23 8447 1 8447 26 4032 2 8393.5 27 3881 2 8242.5 30 8136 1 8136 29 3763 2 8124.5 28 3748 2 8109.5 25 第六节 尺度检验 3 3731 2 8092.5 24 3715 2 8076.5 21 3715 2 8076.5 20 7730 1 7730 17 3313 2 7674.5 16 2901 2 7262.5 13 2732 2 7093.5 12 6834 1 6834 9 2093 2 6454.5 8 5500 1 5500 5 5345 1 ...