自动控制原理期末考试题4

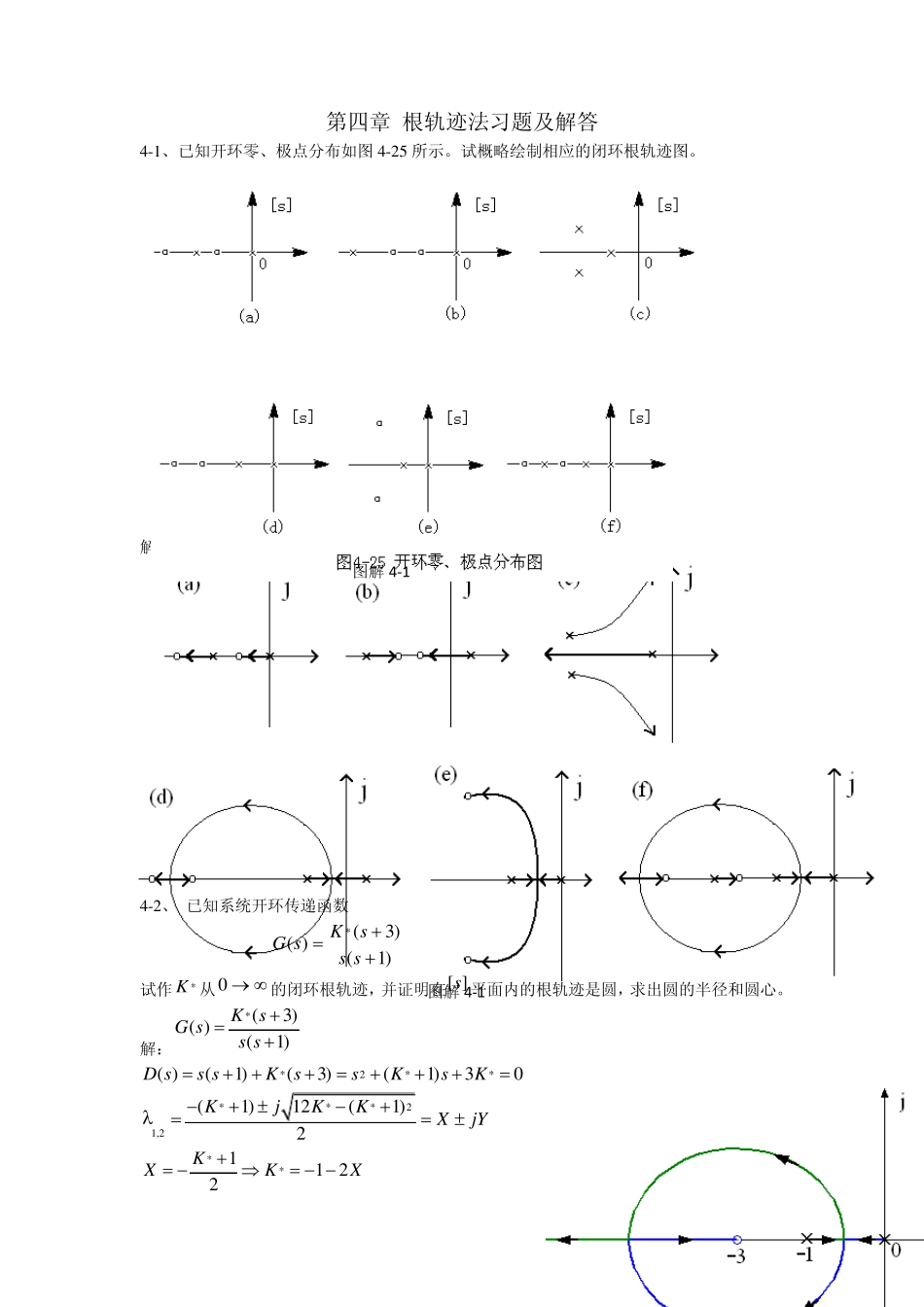
第四章 根轨迹法习题及解答 4-1、已知开环零、极点分布如图 4-25 所示。试概略绘制相应的闭环根轨迹图。 解：根轨迹如图解4-1 所示。 4-2、 已知系统开环传递函数 )1()3()(*sssKsG 试作*K 从0   的闭环根轨迹，并证明在[ ]s 平面内的根轨迹是圆，求出圆的半径和圆心。 解：*(3)( )(1)KsG ss s *2**( )(1)(3)(1)30D ss sKssKsK ***21,2(1)12(1)2KjKKXjY **1122KXKX    图解4-1 图解4-1 **22221 2(1 )1 2 ( 12)( 121 )44(3 )6KKXXYX     22(3 )6XY 根轨迹圆心( 3 ,0 )，半径6 的圆，如图解4 -2 所示。。 4 -3 、设单位反馈控制系统开环传递函数如下，试概略绘出系统根轨迹图（要求确定分离点坐标d ）。 （1 ） )15.0)(12.0()(sssKsG （2 ） )3)(2()5()(*ssssKsG 解 ⑴ )2)(5(1 0)15.0)(12.0()(sssKsssKsG 系统有三个开环极点：01 p,22p,53p ① 实轴上的根轨迹： 5,, 0,2 ② 渐近线： ,33)12(373520kaa ③ 分离点： 021511ddd 解之得： 8 8.01d， 7 8 6 3.32 d(舍去)。 ④ 与虚轴的交点：特征方程为 010107)(23kssssD 令 010)](Im [0107)](Re[32jDkjD 解得710k 与虚轴的交点（0，j10）。 根轨迹如图解4-3(a)所示。 ⑵ 根轨迹绘制如下： ① 实轴上的根轨迹：3,5 , 0,2 ② 渐近线： 22)12(02)5(320kaa ③ 分离点： 5131211dddd 用试探法可得 886.0d。根轨迹如图解4-3(b)所示。 4-4、已知单位反馈系统的开环传递函数如下，试概略绘出系统的根轨迹图（要求算出出射角）。 （1） )21)(21()2()(*jsjssKsG （2） )1010)(1010()20()(*jsjsssKsG 解 ⑴ )21)(21()2()(*jsjssKsG 根轨迹绘制如下： ① 实轴上的根轨迹： 2, ② 分离点：21211211djdjd 解之得： 23.4d ③ 起始角： 43.15390435.631801p 由对称性得另一起始角为 43.153。 根轨迹如图解 4-4(a)所示。...