自动控制原理第5章练习题

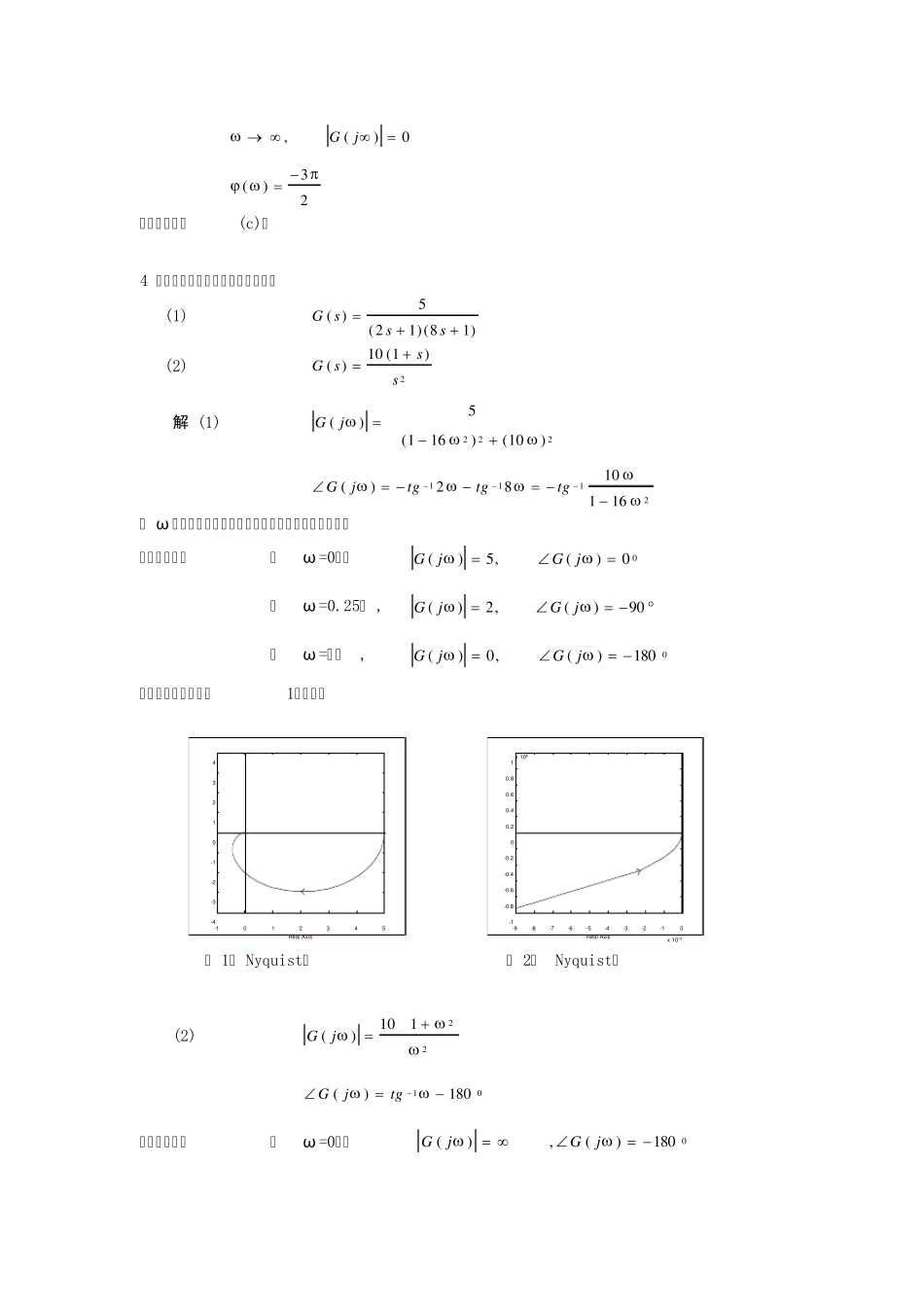
1 某系统结构图如图1所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs （ 1） ttr2sin)( （ 2） )452cos(2)30sin()(tttr 解 系统闭环传递函数为: 21)(ss 图 1 系统结构图 频率特性: 2244221)(jjj 幅频特性: 241)(j 相频特性: )2arctan()( （ 1）当ttr2sin)(时 , 2， rm=1 则 ,35.081)(2j 45)22arctan()2(j )452sin(35.0)2sin()2(ttjrcmss （ 2） 当 )452cos(2)30sin()(tttr时 : 2,21,12211mmrr 5.26)21arctan()1(45.055)1(jj )]2(452cos[)2()]1(30sin[)1()(jtjrjtjrtcmms )902cos(7.0)4.3sin(4.0tt 2 若系统单位阶跃响应 )0(8.08.11)(94teethtt 试求系统频率特性。 解 ssRsssssssC1)(,)9)(4(3 698.048.11)( 则 )9)(4(3 6)()()(ssssRsC 频率特性为 )9)(4(3 6)(jjj 3 绘制下列传递函数的幅相曲线： ( )( )/1G sKs ( )( )/22G sKs ( )( )/33G sKs 解 ( )( )()12GjKjK ej   00,()Gj   ,()Gj0  ()  2 幅频特性如图(a)。 ( )()()()222GjKjK ej   00,()Gj   ,()Gj0  ()   幅频特性如图(b)。 ( )()()()33332GjKjK ej   00,()Gj   ,()Gj0  ()  32 幅频特性如图(c)。 4 试绘制下列传递函数的幅相曲线。 (1) G sss( )()()52181 (2) G sss( )()1 012 解 (1) Gj()()()511 61 0222   Gjtgtgtg()1112281 011 6 取 ω 为不同值进行计算并描点画图，可以作出准确图形 三个特殊点： ① ω =0时， 00)(,5)(jGjG ② ω =0.25时 , 9 0)(,2)(jGjG ③ ω =∞时, 01 8 0)(,0)(jGjG 幅相特性曲线如图（1）所示。 -1012345-4-3-2-101234Real Ax is -9-8-7-6-5-4-3-2-10x 1014-1-0.8-0.6-0.4-0.200.20.40.60.81x 108Real Ax is （ 1） Nyquist图 （ 2） Nyquist...