船舶原理例题1

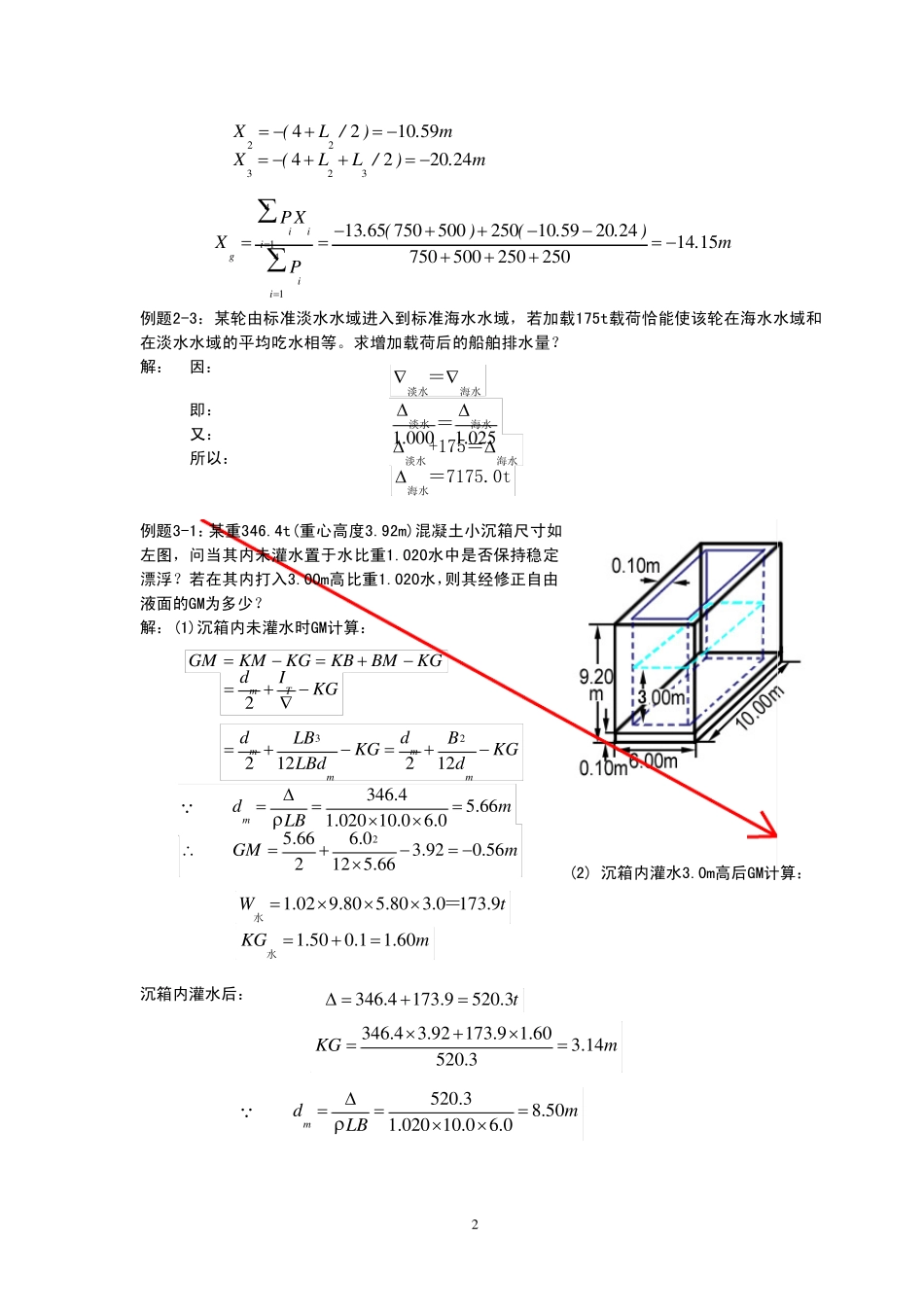
1 《船舶原理基础》例题一 一、计算题 例题1-1：计算图示船舶的各种船形系数： 解： 水线面面积系数Cw =1.0 船中剖面系数Cm =0.5 方形系数Cb =0.5 棱形系数Cp =1.0 垂向棱形系数Cvp =0.5 例题1-2、例题1-3见讲义。 例题2-1：已知某轮船长148m，某装载状态下D = 19000t，首吃水8.55m，尾吃水9.05m，水密度1.008g/cm3。试求该轮航行至水密度为1.023g/cm3水域时的首尾吃水各为多少？(设此时Xf=-4.20m,TPC = 25.5t/cm) 解： 因：mTPCds1 1.0)0 0 8.110 2 3.11(5.2 51 0 00 2 5.11 9 0 0 0)11(1 0 001−=−××=−Δ=ρρρδ 所以： mdmdAF9 4.81 1.00 5.94 4.81 1.05 5.8=−==−= 例题2-2：某轮第四舱底舱积载计划如右图,铝矾土500t (SF4 = 0.91 m3/t),纸250t (SF2 = 2.69 m3/t)，重烧镁250t(SF3= 1.25m3/t)，苦杏仁750t(SF1 =1.98 m3/t)。该舱长19.3m，前舱壁距船中为-4.0 m，试求每票货和全舱货物的重心距中距离？ 解：设四票货距中距离分别为X1、X2、X3和X4。 显然： 141 9 34 01 3 6 52.XX(. ).m== −+= − 22222331 9 31 3 1 8P SFL..mP SFP SF==+ 321 9 36 1 2L.L.m=−= 222323421 0 5 9422 0 2 4X(L /).mX(LL /).m= −+= −= −++= − 41411 3 6 5 7 5 05 0 02 5 01 0 5 92 0 2 41 4 1 57 5 05 0 02 5 02 5 0iiigiiPX.()(..)X.mP==−++−−=== −+++∑∑ 例题2-3：某轮由标准淡水水域进入到标准海水水域，若加载175t载荷恰能使该轮在海水水域和在淡水水域的平均吃水相等。求增加载荷后的船舶排水量？ 解： 因： 即： 又： 所以： 例题3-1：某重346.4t(重心高度3.92m)混凝土小沉箱尺寸如左图，问当其内未灌水置于水比重1.020水中是否保持稳定 漂浮？若在其内打入3.00m高比重1.020水，则其经修正自由液面的GM为多少？ 解：(1)沉箱内未灌水时GM计算： (2) 沉箱内灌水3.0m高后GM计算： 沉箱内灌水后： ∇∇淡水海水＝1 .0 0 01 .0 2 5ΔΔ淡水海水＝ΔΔ淡水海水+175＝Δ海水＝7175.0tGMKMKGKBBMKG=−=+−2mTdIKG=+−∇3221 221 2mmmmddLBBKGKGLBdd=+−=+−3 4 6 .45 .6 61 .0 2 01 0 .06 .0mdmLBρΔ===××Q25 .6 66 .03 .9 20 .5 621 25 .6 6GMm∴=+−= −×1 .0 29 .8 05 .8 03 .01 7 3 .9Wt=×××水＝1 .5 00 .11 .6 0KGm=+=水3 4 6 .41 7...