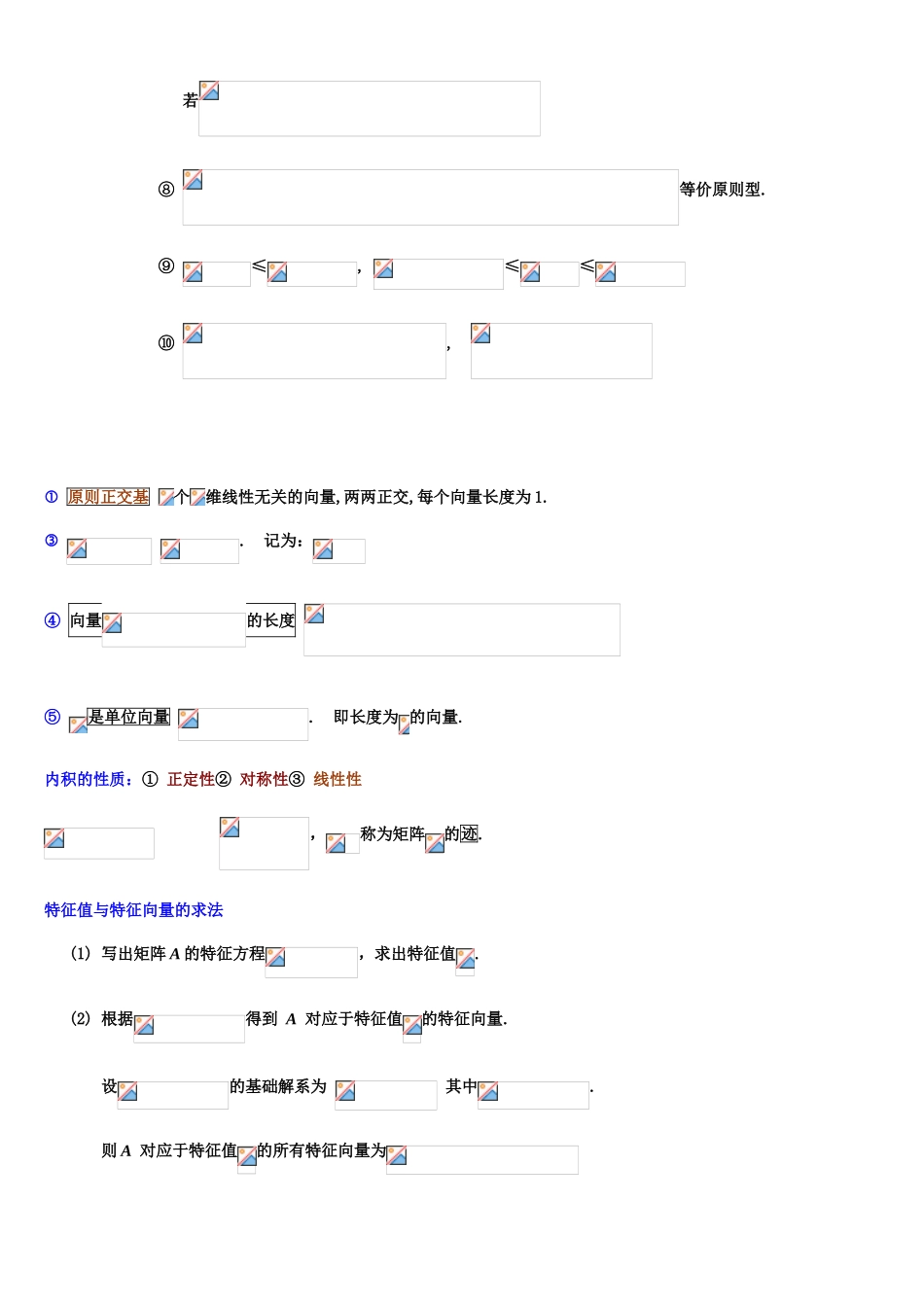
范德蒙德行列式:代数余子式和余子式的关系:分块对角阵相乘:, 分块矩阵的转置矩阵: ,为中各个元素的代数余子式.,, .分块对角阵的伴随矩阵: 矩阵的秩的性质: ① ≥ ; ;≤≤ ④ ⑤ ≤⑥ 若、可逆,则; 即:可逆矩阵不影响矩阵的秩. ⑦ 若;矩 阵 转 置 的 性质:矩 阵 可 逆 的 性质:伴 随 矩 阵 的 性质:(无条件恒成立) 若⑧ 等价原则型.⑨ ≤, ≤≤⑩ , 原则正交基 个维线性无关的向量,两两正交,每个向量长度为 1. . 记为:④ 向量的长度 ⑤ 是单位向量 . 即长度为 的向量.内积的性质:① 正定性② 对称性③ 线性性 ,称为矩阵的迹.特征值与特征向量的求法 (1) 写出矩阵 A 的特征方程,求出特征值. (2) 根据得到 A 对应于特征值的特征向量. 设的基础解系为 其中. 则 A 对应于特征值的所有特征向量为 其中为任意不全为零的数. 3. 与相似 (为可逆矩阵) 与正交相似 (为正交矩阵) 可以相似对角化 与对角阵相似.(称是的相似原则形)7. 矩阵对角化的判定措施 ① n 阶矩阵 A 可对角化 (即相似于对角阵) 的充足必要条件是 A 有 n 个线性无关的特征向量. 这时,为的特征向量拼成的矩阵,为对角阵,主对角线上的元素为的特征值. 设为对应于的线性无关的特征向量,则有:. ② 可相似对角化,其中为的重数恰有个线性无关的特征向量. :当为的重的特征值时,可相似对角化的重数基础解系的个数. ③ 若阶矩阵有个互异的特征值可相似对角化.正交矩阵 ③ 正交阵的行列式等于 1 或-1;⑤ 两个正交阵之积仍是正 交阵;⑥ 的行(列)向量都是 单位正交向量组.施密特正交规范化 线性无关, 单位化: 1. 二次型 其中为对称矩阵, 与协议 . ()求 C (A I)→(B C^T) 这个变换先进行行变换 再进行一致的列变换 最终 求得 C 和 C^T 正惯性指数 二次型的规范形中正项项数 负惯性指数二次型的规范形中负项项数 ④ 两个矩阵协议它们有相似的正负惯性指数他们的秩与正惯性指数分别相等. ⑤ 两个矩阵协议的充足条件是:与等价 ⑥ 两个矩阵协议的必要条件是:2. 通过 化为原则形. 正交变换法 配措施(1)若二次型具有的平方项,则先把具有的乘积项集中,然后配方,再对其他的变量同样进行, 直到都配成平方项为止,通过非退化线性变换,就得到原则形;(2) 若二次型中不具有平方项,不...