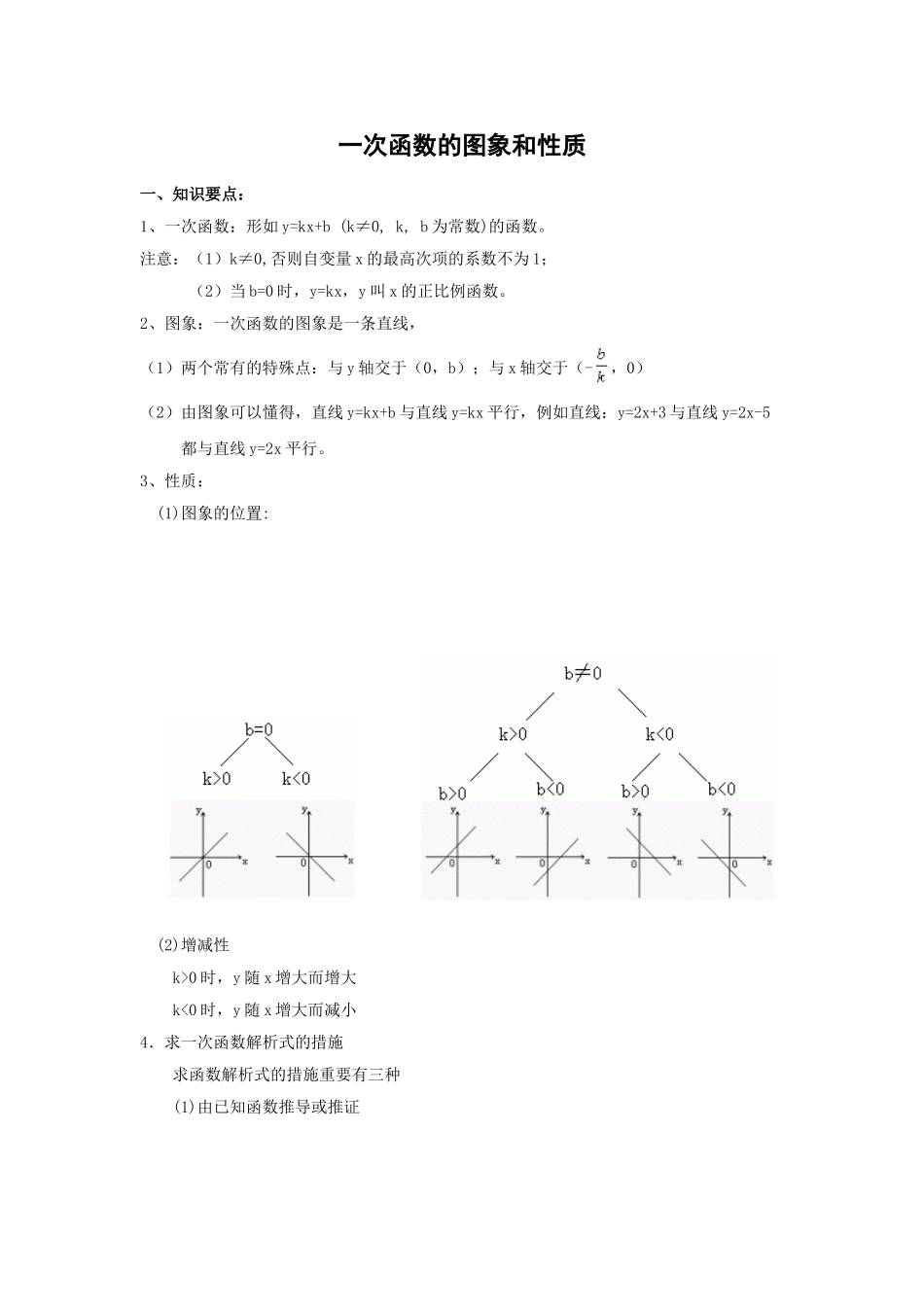
一次函数的图象和性质一、知识要点: 1、一次函数:形如 y=kx+b (k≠0, k, b 为常数)的函数。 注意:(1)k≠0,否则自变量 x 的最高次项的系数不为 1; (2)当 b=0 时,y=kx,y 叫 x 的正比例函数。 2、图象:一次函数的图象是一条直线, (1)两个常有的特殊点:与 y 轴交于(0,b);与 x 轴交于(-,0) (2)由图象可以懂得,直线 y=kx+b 与直线 y=kx 平行,例如直线:y=2x+3 与直线 y=2x-5都与直线 y=2x 平行。 3、性质: (1)图象的位置: (2)增减性 k>0 时,y 随 x 增大而增大 k<0 时,y 随 x 增大而减小 4.求一次函数解析式的措施 求函数解析式的措施重要有三种 (1)由已知函数推导或推证 (2)由实际问题列出二元方程,再转化为函数解析式,此类题一般在没有写出函数解析式前无法(或不易)判断两个变量之间具有什么样的函数关系。 (3)用待定系数法求函数解析式。 “待定系数法”的基本思想就是方程思想,就是把具有某种确定形式的数学问题,通过引入某些待定的系数,转化为方程(组)来处理,题目的已知恒等式中具有几种等待确定的系数,一般就需列出几种具有待定系数的方程,本单元构造方程一般有下列几种状况: ①运用一次函数的定义 构造方程组。 ②运用一次函数 y=kx+b 中常数项 b 恰为函数图象与 y 轴交点的纵坐标,即由 b 来定点;直线 y=kx+b 平行于 y=kx,即由 k 来定方向 。 ③运用函数图象上的点的横、纵坐标满足此函数解析式构造方程。 ④ 运用题目已知条件直接构造方程 。二、例题举例: 例 1.已知 y=,其中=(k≠0 的常数),与成正比例,求证 y 与 x 也成正比例。 证明: 与成正比例, 设=a(a≠0 的常数), y=, =(k≠0 的常数), ∴y=·a=akx, 其中 ak≠0 的常数, ∴y 与 x 也成正比例。 例 2.已知一次函数=(n-2)x+-n-3 的图象与 y 轴交点的纵坐标为-1,判断=(3-)是什么函数,写出两个函数的解析式,并指出两个函数在直角坐标系中的位置及增减性。 解:依题意,得 解得 n=-1, ∴=-3x-1, =(3-)x, 是正比例函数; =-3x-1 的图象通过第二、三、四象限,随 x 的增大而减小; =(3-)x 的图象通过第一、三象限,随 x 的增大而增大。 阐明:由于一次函数的解析式具有待定系数 n,故求解析式的关键是构造有关 n 的方程,此题运用“一次函数解析式的常数项就是图象与 y 轴交点纵坐标”来构造方程。 例 3...