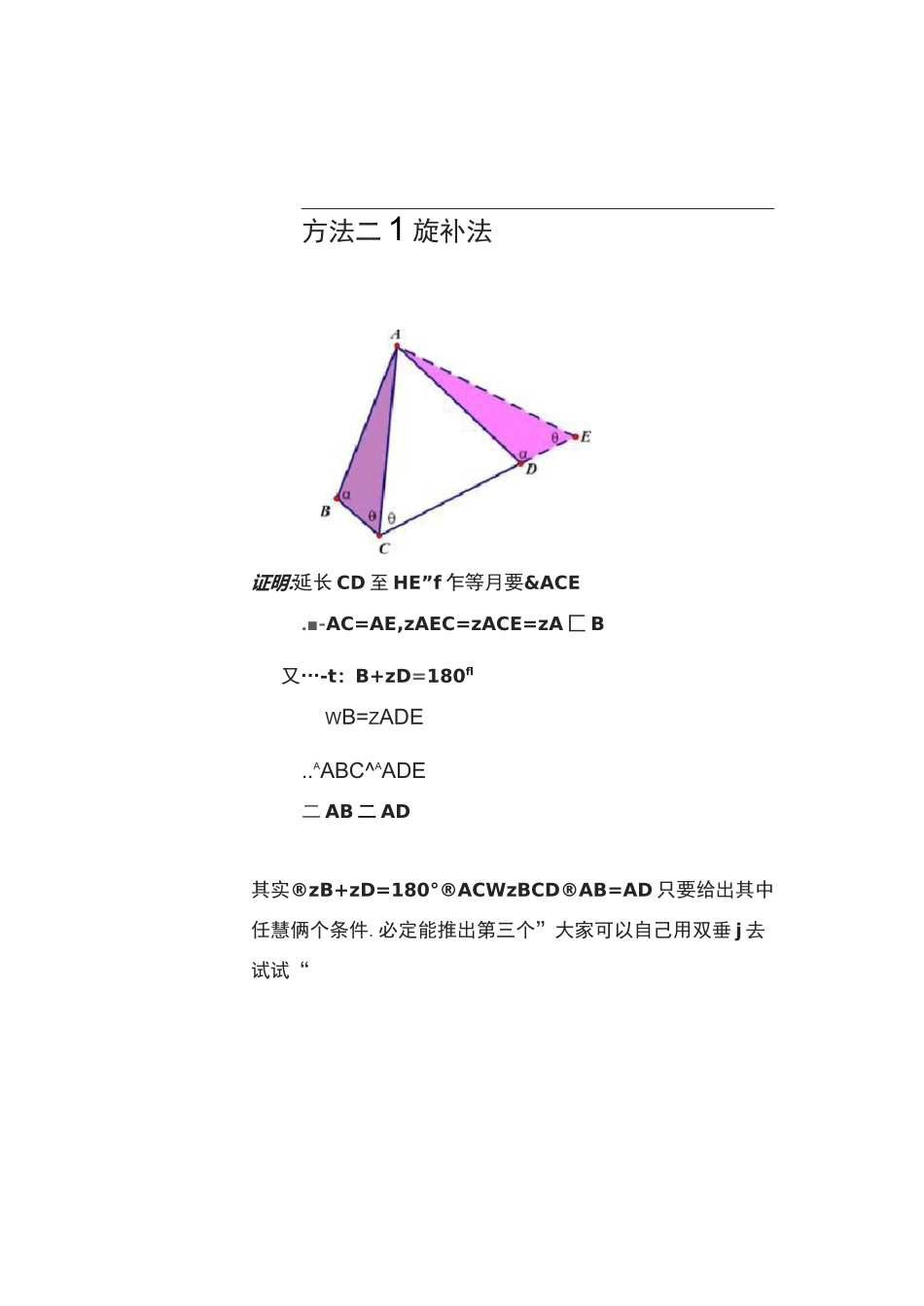
初中数学 I 对角互补+角平分线模型对角互补+角平分线模型已知,四边形 A 吕 CD,ZB+ZD=18CQ,AC 平分 ZBCD结论① AB=AD结论①的证明存三种方法1 四点共圆 2 双垂法 3 旋补法其中双垂法是一种通法,有些变型题 I 其他俩种方法不好解决,但双垂法百试不爽。下面,我介绍双垂法和旋补法°方法一 2 双垂法证明:分别过 A 作 CD 和 CB 得垂线 AM 和 ANVA€平分 ZBCDAAM=AiM又 VZB^ZD=180°AZABN^ZDAABN^AADM;-AB=AD方法二 1 旋补法证明:延长 CD 至 HE”f 乍等月要&ACE.■-AC=AE,zAEC=zACE=zA 匚 B又…-t:B+zD=180flWB=ZADE..AABC^AADE二 AB 二 AD其实®zB+zD=180°®ACWzBCD®AB=AD 只要给出其中任慧俩个条件.必定能推出第三个”大家可以自己用双垂 j 去试试“已知,ABCD,^B4-ZD=180°tAC 平分^BCD 结论② BC+CD=2ACcos6证明:过 A 作 AF 丄 CD由结论①可知:汕 CE 为等腰三角形,且 BUDE..BC+CD=CE=2CF又…CF=ACme..BC+CD=2CF=2ACcos6已知,ABCD,^B+ZD=180°tAC 平分^BCD结论③四边形 ABCD 的面积三等腰三角形 ACE 的面积=AC3&inBcosE1 黄空绿,把黄割补到绿的位置二四边形 ABCD 的面积二等腰三荊形 ACE 的面积VACE 的面积=AF*CF(其中 AF^ACsin0XF=ACcos6)四边形 ABCD 的面积二等腰三角形 ACE 的面积=AC2sin9cos9特别地』^zBCD=120°B 寸』BC+CD=2ACcos60fl=AC四边形 ABCO 面积=正三角形 ACE 面积AC特另 U 地,当疋 BCD 二勺 0°时,BC+CD-2ACcos45fl-^AC四边形 ABCD 通积二等腰直角三角形 ACE 面积