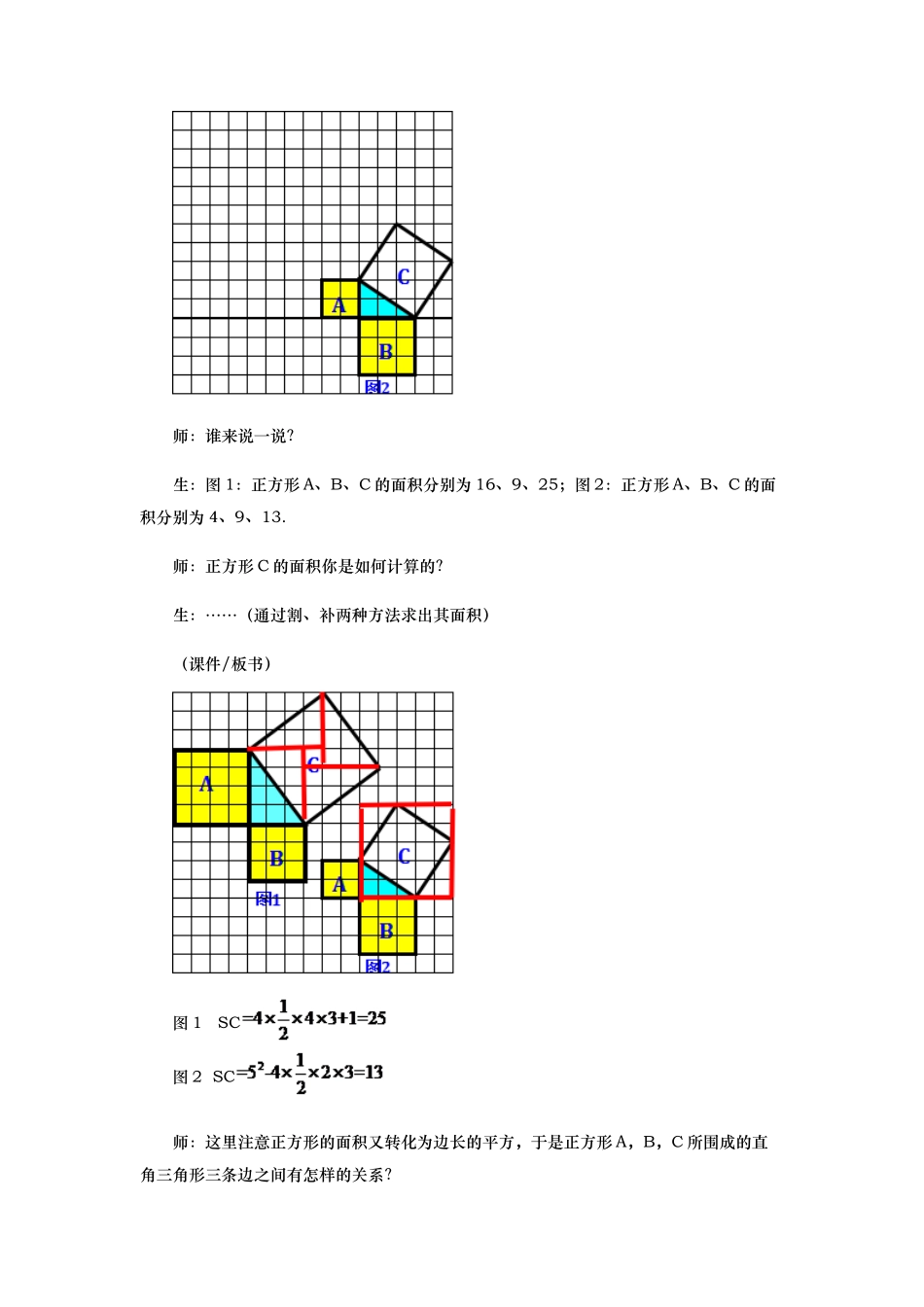
教学准备 1. 教学目标 1.1 知识与技能:通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论.1.2 过程与方法:1.在充分观察、归纳、猜想、探究直角三角形两条直角边的平方和等于斜边的平方的过程中,进展合情推理能力,体会数形结合的思想.2.在探究上述结论的过程中,进展归纳、概括和有条理地表达活动的过程和结论.1.3 情感态度与价值观:1.树立积极参加、合作沟通的意识.2.在探究勾股定理的过程中,体验获得结论的欢乐,锻炼克服困难的勇气.2. 教学重点/难点 2.1 教学重点:探究直角三角形两条直角边的平方和等于斜边的平方的结论,从而发现勾股定理.2.2 教学难点:以直角三角形的边为边的正方形面积的计算.3. 教学用具 4. 标签 教学过程 1 谈话引入我们知道,讨论三角形从它的元素入手,也就是三角形的三条边和三个角。对于等腰三角形和等边三角形的边,除满足三边关系定理外,它们还分别存在着两边相等和三边相等的特别关系。那么对于直角三角形的边,除满足三边关系定理外,它们之间也存在着特别的关系,这就是我们这一节要讨论的问题:勾股定理.推动新课(板书课题:勾股定理)2 新知探究问题 1 相传 2500 多年前,古希腊著名的哲学家、数学家、天文学家,毕达哥拉斯有一次在朋友家作客,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.观察下面图中的地面,看看你能发现什么?三个正方形 A,B,C 的面积有什么关系?师:同学们,我们也来是否也和大哲学家有同样的发现呢?观察三个正方形之间的面积的关系.生:两个小正方形的面积之和等于大正方形的面积.师:为什么?生:……(通过直接数等腰直角三角形的个数,或者用割补的方法将小正方形 A,B中的等腰直角三角形补成一个大正方形,得出结论:小正方形 A,B 的面积之和等于大正方形 C 的面积.)师:这里每个正方形的面积等于其边长的平方.于是这三个正方形的边长构成的等腰直角三角形三条边长之间有怎样的特别关系?生:等腰直角三角形两条直角边的平方和等于斜边的平方.师:等腰直角三角形是特别的直角三角形,接下来探究问题 2.问题 2 在网格中的一般的直角三角形,以它的三边为边长的三个正方形 A,B,C 的面积是否也有类似的关系?师:如图, 以直角三角形的三边为边长作三个正方形 A、B、C,并计算他们的面积.(学生动手计算,老师巡视指导)师:谁来说一说?生:图 1:正方形 A、B、C 的...