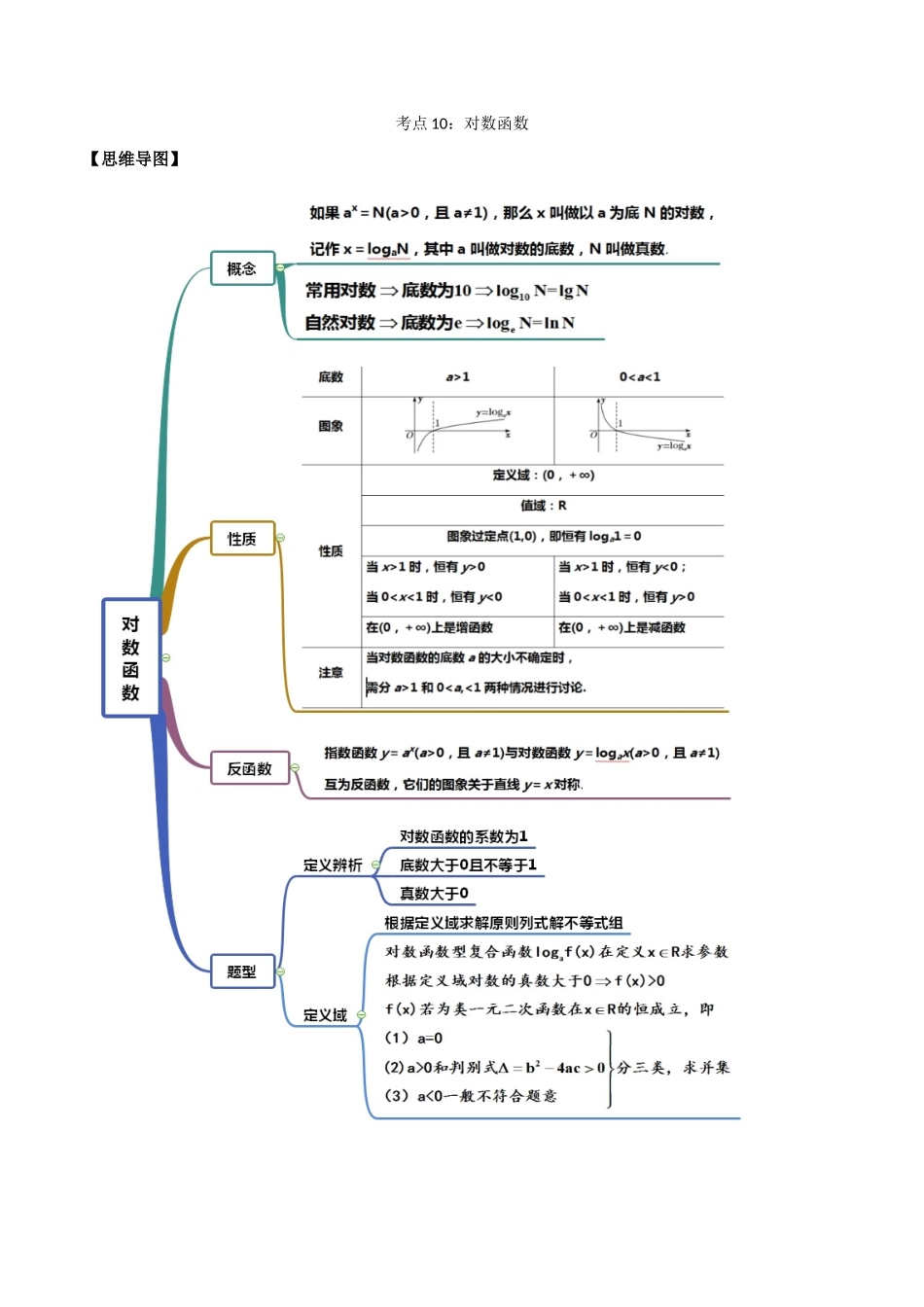
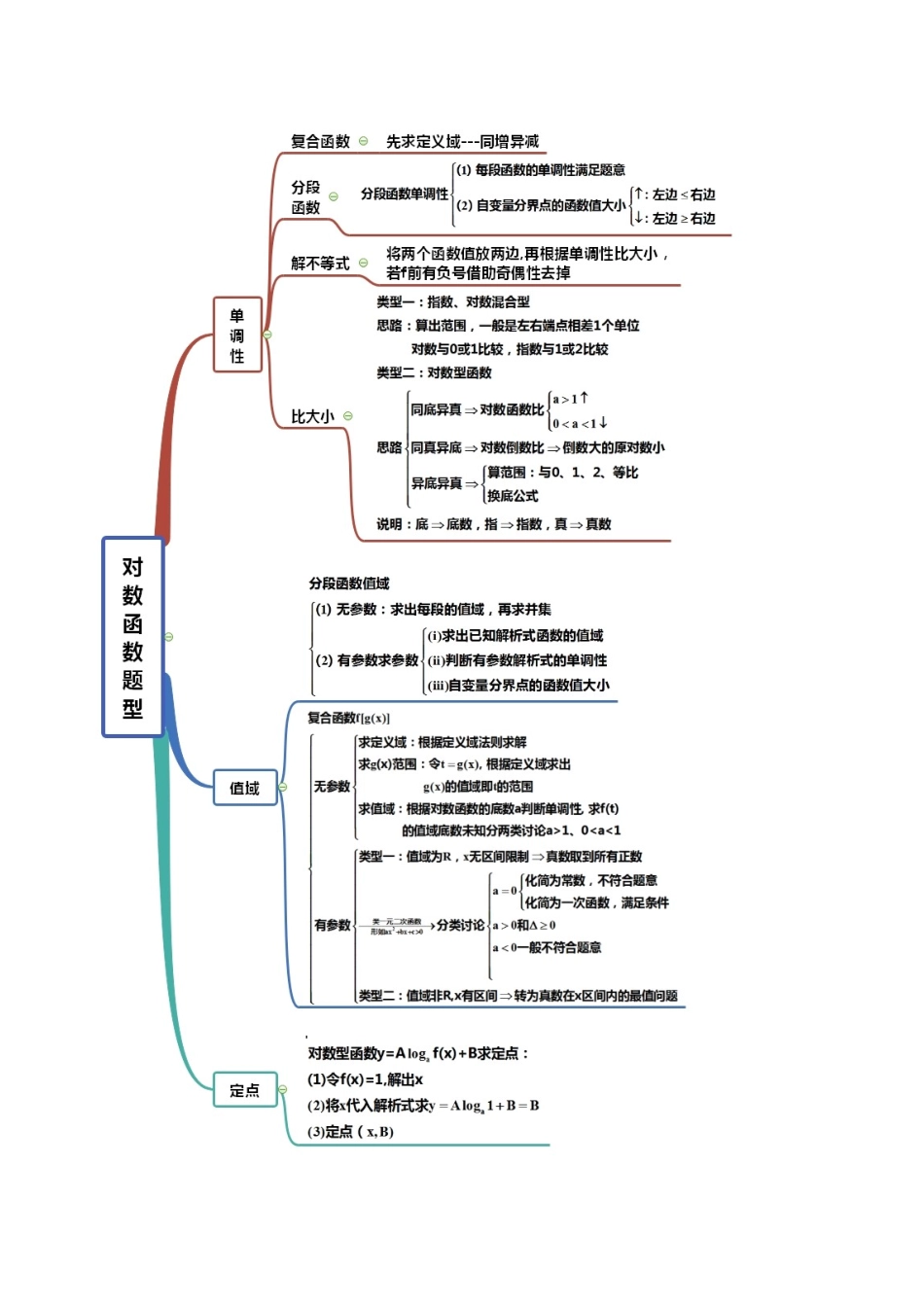
考点 10:对数函数【思维导图】【常见考法】考法一:定义辨析1.下列函数表达式中,对数函数的个数有 。①;②;③;④;⑤;⑥;⑦.【答案】2【解析】由于①中自变量出现在底数上,①不是对数函数;由于②中底数不能保证,且,②不是对数函数;由于⑤⑦的真数分别为,,⑤⑦也不是对数函数;由于⑥中的系数为 2,⑥也不是对数函数;只有③④符合对数函数的定义.2.若函数是对数函数,_________.【答案】5【解析】由对数函数的定义可知,,解得.故答案为:考法二:定义域1.函数的定义域是 。【答案】【解析】由题意可知:.2.函数的定义域是 。【答案】(-1,0 ]【解析】由题意可得:且,解得且 x≤0 ,所以定义域为 (-1,0 ].3.已知函数,则函数的定义域为 。【答案】【解析】对于函数,,即,解得.对于函数,有,解得.因此,函数的定义域为.4.函数 f(x)=lg(1+2cosx)的定义域为 。【答案】 【解析】由题意得,所以,即得 5.函数的定义域为,则实数的取值范围是 。【答案】【解析】 的定义域为,∴恒成立,即判别式,得,即实数的取值范围是6.若函数的定义域为 R,则实数 m 的取值范围是 。【答案】【 解 析 】 试 题 分 析 : 函 数的 定 义 域 是 R , 则 有恒 成 立 . 设,当时, 恒成立;当时,要使得恒成立,则有,解得.所以实数的取值范围是.考法三:单调性1.函数的单调递减区间为 。【答案】【解析】由得,或,则函数的定义域为,又函数在上单调递减,在上单调递增,函数在上单调递增,由复合函数的单调性原则“同增异减”得函数的单调递减区间为2.函数的单调递增区间为 。【答案】【解析】函数所以定义域为,解得或 由复合函数“同增异减”的性质,可知函数的单调递增区间为即为函数的单调递增区间3.已知函数(其中,)在区间上单调递减,则实数的取值范围是 。 【答案】【解析】函数 y=loga(8﹣ax)(其中 a>0,a≠1)在区间[1,4]上单调递减,当 a>1 时,由函数 t=8﹣ax 在区间[1,4]上单调递减且 t>0,故 84﹣ a>0,求得 1<a<2.当 0<a<1 时,由函数 t=8﹣ax 在区间[1,4]上单调递减,可得函数 y=loga(8﹣ax)在区间[1,4]上单调递增,这不符合条件.综上,实数 a 的取值范围为(1,2)。4.若 f(x)=ln(x2-2ax+1+a)在区间上递减,则实数的取值范围为 。【答案】【解析】令,其对称轴方程为,外函数对数函数是增函数,要使函数在上递减,则,即:...