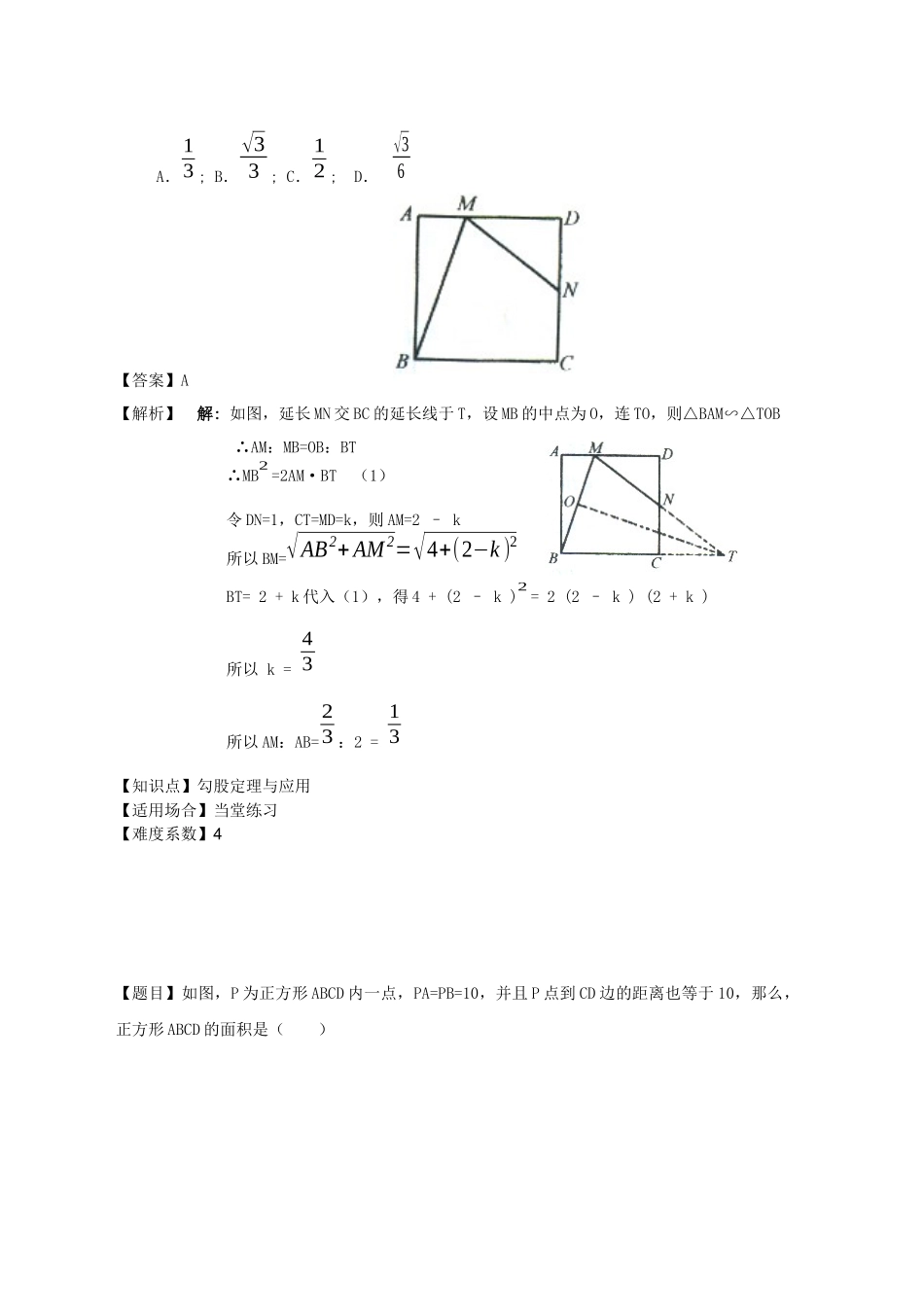
勾股定理与应用知识定位三解形是平面几何中最重要的图形,它的有关知识是今后我们学习四边形、多边形乃至立体几何的重要基础,而其中的勾股定理在初中竞赛三角形中占据非常大的地位。必须熟练掌握勾股定理及逆定理的应用、勾股数的推算公式和判定直角三角形。本节我们通过一些实例的求解,旨在介绍数学竞赛中勾股定理中相关问题的常见题型及其求解方法本讲将通过例题来说明这些方法的运用。 知识梳理1、勾股定理及逆定理:ABC△中 ∠C=Rt∠⇔ a2+b2=c22、勾股定理及逆定理的应用① 作已知线段 a 的√2,√3, √5……倍② 计算图形的长度,面积,并用计算方法解几何题③ 证明线段的平方关系等。3、勾股数的定义:假如三个正整数 a,b,c 满足等式 a2+b2=c2,那么这三个正整数 a,b,c 叫做一组勾股数.4、勾股数的推算公式④ 罗士琳法则任取两个正整数 m 和 n(m>n),那么 m2-n2,2mn, m2+n2是一组勾股数。⑤ 假如 k 是大于 1 的奇数,那么 k, k2−12,k2+12是一组勾股数。⑥ 假如 k 是大于 2 的偶数,那么 k, (K2 )2−1,(K2 )2+1是一组勾股数。⑦ 假如 a,b,c 是勾股数,那么 na, nb, nc (n 是正整数)也是勾股数。5、 熟悉勾股数可提高计算速度,顺利地判定直角三角形简单的勾股数有:3,4,5; 5,12,13; 7,24,25; 8,15,17; 9,40,41。常见勾股数 3,4,5 : 勾三股四弦五 5,12,13 : 5·12 记一生 6,8,10: 连续的偶数 7,24,25 : 企鹅是二百五8,15,17 : 八月十五在一起特别勾股数 连续的勾股数只有 3,4,5连续的偶数勾股数只有 6,8,102.100 以内的勾股数开头数字为 20 以内3 4 5;5 12 13; 6 8 10;7 24 25;8 15 17;9 12 15;9 40 41;10 24 26;11 60 61;12 16 20;12 35 37;13 84 85;14 48 50;15 20 25;15 36 39;16 30 34;16 63 65;18 24 30;18 80 82例题精讲【题目】△ABC 周长是 24,M 是 AB 的中点 MC=MA=5,则△ABC 的面积是多少【答案】24【解析】 解: MA=MB=MC=5, ∴∠ACB=90°知周长是 24,则 AC+BC=14,AC2 +BC2 =102 ,∴2AC·BC=(AC+BC)2 -(AC2 +BC2 ) = 142 -102=4×24∴SΔ ABC=12 AC⋅BC=24【知识点】勾股定理与应用【适用场合】当堂例题【难度系数】2【题目】如图 1,在正方形 ABCD 中,N 是 CD 的中点,M 是 AD 上异于 D 的点,且∠NMB=∠MBC...