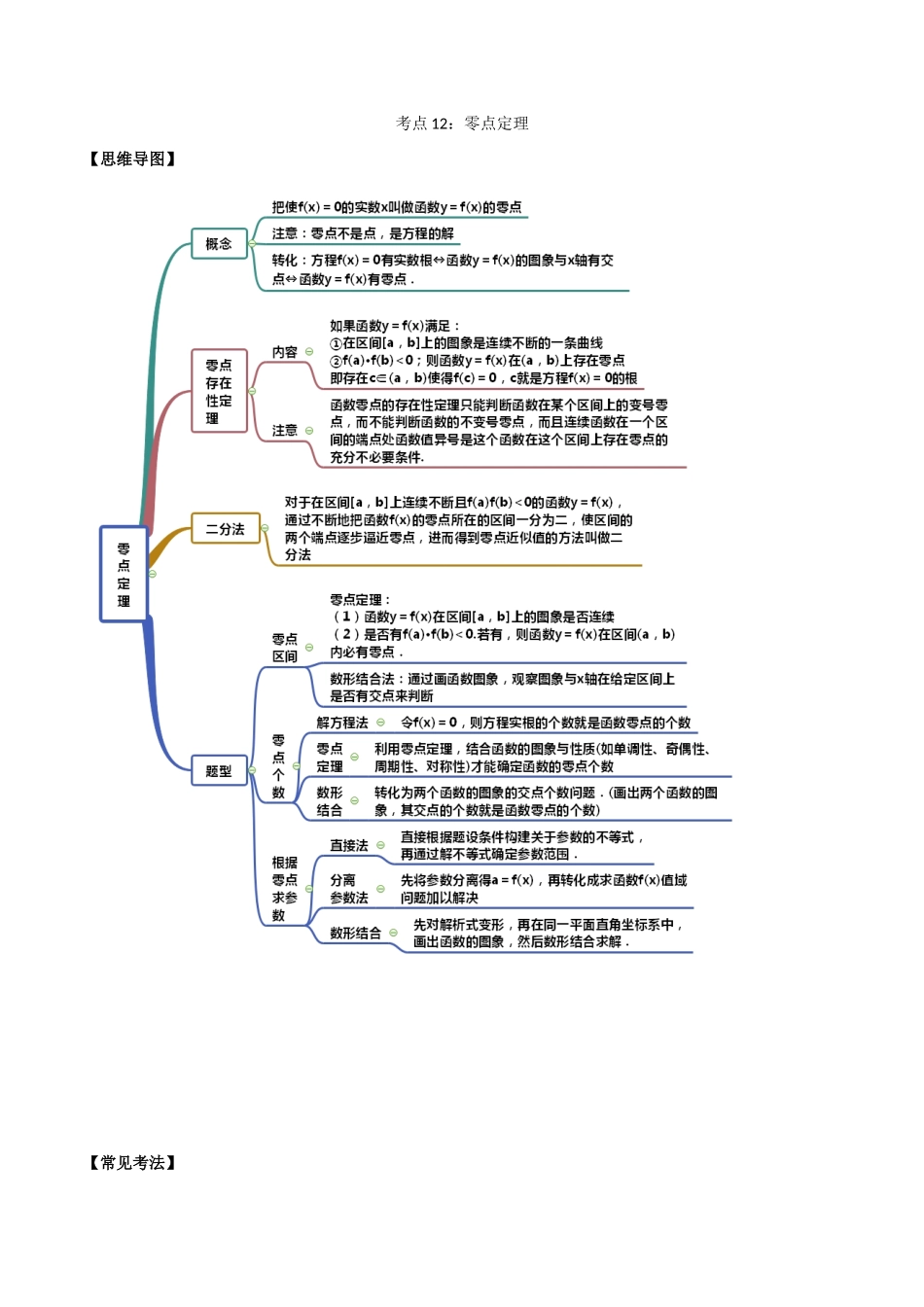
考点 12:零点定理【思维导图】【常见考法】考点一:求零点1.若幂函数的图象过点,则函数的零点是 。【答案】9【解析】 幂函数的图象过点,∴,解得,∴∴由,得.2.函数的零点是____________.【答案】【解析】令 f(x)=0,即 x2+3x-4=0,解得:x=-4,x=1.3.若函数,则函数的零点是___________.【答案】0 或【解析】要求函数的零点,则令,即,又因为:,① 当时,,,解得.② 当时,,,解得(负值舍去),所以.综上所以,函数的零点是 0 或.故答案为:0 或4.函数 y=的图象与函数 y=2sinπx(-2≤x≤4)的图象所有交点的横坐标之和等于 .【答案】8【解析】函数 y1=与 y2=2sinπx 的图象有公共的对称中心(1,0),作出两个函数的图象,由图象可知,两个函数在[-2,4 上共有 8 个交点,两两关于点(1,0)对称设对称的两个点的横坐标分别为 m、n 则 m+n=2×1=2,故所求的横坐标之和为 8,故答案为 8.考点二:零点区间1.函数的零点所在区间是( )A.B.C.D.【答案】D【解析】易知函数为减函数,又,,根据零点存在性原理,可知函数的零点所在的区间是,故选 D.2.函数的零点所在的区间为( )A.B.C.D.【答案】B【解析】 函数单调递增,∴f(0)=-4,f(1)=-1,f(2)=7>0,根据零点的存在性定理可得出零点所在的区间是,故选 B.3.函数的零点所在的区间为( )A.B.C.D.【答案】C【解析】 f(x)=lnx+x-3 在(0,+∞)上是增函数f(1)=-2<0,f(2)=ln2-1<0,f(3)=ln3>0∴f(2)•f(3)<0,根据零点存在性定理,可得函数 f(x)=lnx+x-3 的零点所在区间为(2,3)故选:C.4.已知是定义在上的单调函数,满足,则函数的零点所在区间为( )A.B.C.D.【答案】C【解析】设,即,,因为是定义在上的单调函数,所以由解析式可知,在上单调递增.而,,故,即.因为,,由于,即有,所以.故,即的零点所在区间为.故选:C.考点三:零点个数1.函数 f(x)=|x-2|-lnx 在定义域内零点的个数为 。【答案】2【解析】分别画出函数 y=ln x(x>0)和 y=|x-2|(x>0)的图像,可得 2 个交点,故 f(x)在定义域中零点个数为 2.2.方程的解的个数是 。【答案】2【解析】作出和的函数图象,如图所示:由图象可知两函数图象有 2 个交点.故方程的解的个数也为 2 个.3.方程在区间上的解的个数为 。【答案】8【解析】由得,,分别画出和在的图像,如图:两函数图像有 8 个交点,故方程在区间上的解的个数为...