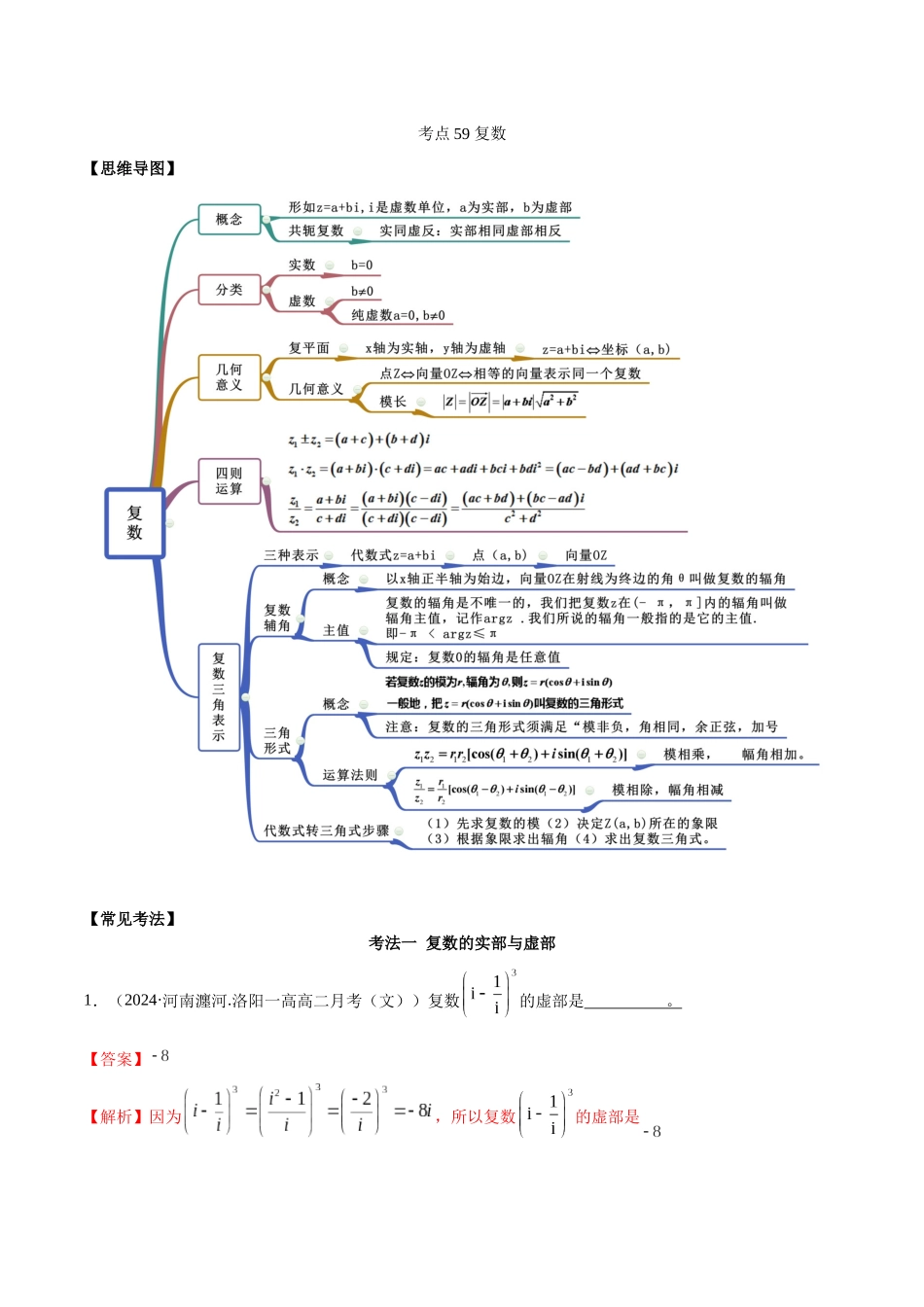
考点 59 复数【思维导图】【常见考法】考法一 复数的实部与虚部1.(2024·河南瀍河.洛阳一高高二月考(文))复数的虚部是 。【答案】【解析】因为,所以复数的虚部是2.(2024·江西景德镇一中高三月考(文))已知复数为纯虚数虚数单位 ,则实数 。【答案】【解析】为纯虚数,,,3.(2024·临猗县临晋中学高二期末(理))已知复数 z 满足,则复数的虚部为 。【答案】-1【解析】设 ,由 , .4.(2024·河南高三其他(理))已知复数,则的虚部是 。【答案】1【解析】由,得,则,其虚部为 1.考法二 复数的几何意义1.(2024·山东聊城)在复平面内,复数所对应的点位于第 象限【答案】二【解析】由题,在复平面内对应的点为,在第二象限2.(2024·兴仁市凤凰中学)已知复数,则复数 z 的共辄复数在复平面上对应的点位于第 象限【答案】四【解析】因为,所以,所以复数 z 的共辄复数在复平面上对应的点为,该点在第四象限.3.(2024·河北石家庄)设复数,则复数在复平面内对应的点的坐标为 。【答案】【解析】因为,所以复数在复平面内对应的点的坐标为.4.(2024·山东临沂)已知复数满足(i 为虚数单位),则(为的共轭复数)在复平面内对应的点位于第 象限【答案】三【解析】由知:∴,即对应的点为5.(2024·全国高三其他(理))已知 i 为虚数单位,且复数 z 满足 ,则复数 z 在复平面内的点到原点的距离为 。【答案】【解析】由,得,∴复数 z 在复平面内的点的坐标为,到原点的距离为.考法三 复数的分类1.(2024·海南枫叶国际学校)若复数为纯虚数为虚数单位 ,则实数 a 的值为________【答案】【解析】是纯虚数,且,解得.故答案为:.2.(2024·山东滨州)已知复数是纯虚数,则实数 m= 。【答案】-1【解析】 是纯虚数,∴ ,解得:3.(2024·陕西新城.西安中学高三月考(文))设, 是虚数单位,则“”是“复数为纯虚数”的( )A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件【答案】B【解析】由复数为纯虚数,则,解得, 所以是复数为纯虚数的充要条件,故选 B.考法四 复数的计算1.(2024·上海高三专题练习)当时, 。【答案】【解析】因为所以所以 ,所2.(2024·全国)若,则的值为 。【答案】【解析】因为,两边同乘,,所以,则,,所以原式.3.(2024·黑山县黑山中学高三其他(理))若复数( 是虚数单位),则在复平面内,的共轭...