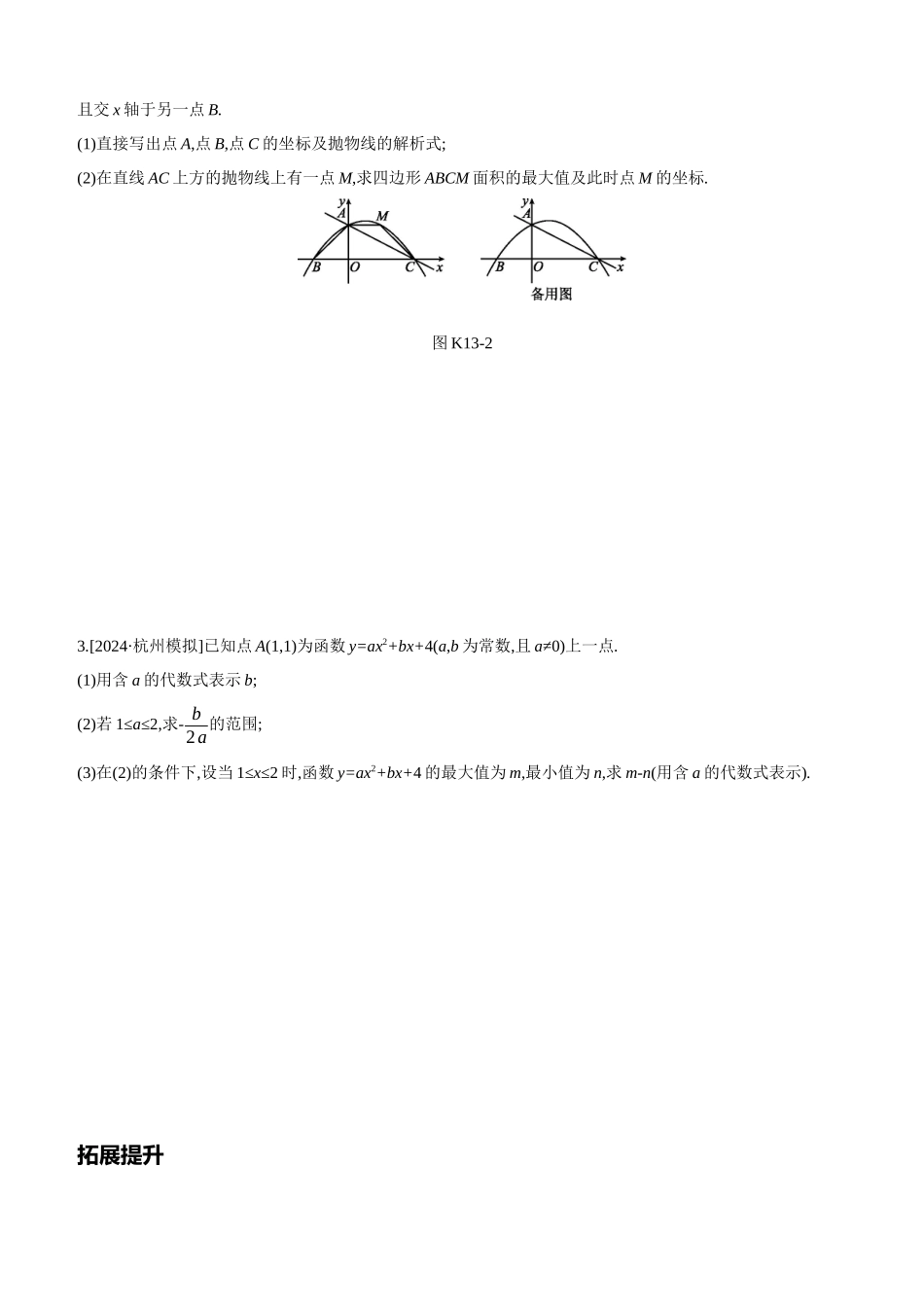
课时训练(十三) 二次函数的综合应用[限时: 分钟] 夯实基础1.[2024·铜仁节选]如图 K13-1,已知抛物线 y=ax2+bx+6 经过两点 A(-1,0),B(3,0),C 是抛物线与 y 轴的交点.(1)求抛物线的解析式;(2)点 P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC 的面积为 S,求 S 关于 m 的函数表达式(指出自变量 m 的取值范围)和 S 的最大值.图 K13-12.[2024·襄阳节选]如图 K13-2,直线 y=-12x+2 交 y 轴于点 A,交 x 轴于点 C,抛物线 y=-14x2+bx+c 经过点 A,点 C,且交 x 轴于另一点 B.(1)直接写出点 A,点 B,点 C 的坐标及抛物线的解析式;(2)在直线 AC 上方的抛物线上有一点 M,求四边形 ABCM 面积的最大值及此时点 M 的坐标.图 K13-23.[2024·杭州模拟]已知点 A(1,1)为函数 y=ax2+bx+4(a,b 为常数,且 a≠0)上一点.(1)用含 a 的代数式表示 b;(2)若 1≤a≤2,求- b2a的范围;(3)在(2)的条件下,设当 1≤x≤2 时,函数 y=ax2+bx+4 的最大值为 m,最小值为 n,求 m-n(用含 a 的代数式表示).拓展提升4.[2024·乐山]已知抛物线 y=ax2+bx+c 与 x 轴交于 A(-1,0),B(5,0)两点,C 为抛物线的顶点,抛物线的对称轴交 x 轴于点 D,连接 BC,且 tan∠CBD=43,如图 K13-3 所示.(1)求抛物线的解析式.(2)设 P 是抛物线的对称轴上的一个动点.① 过点 P 作 x 轴的平行线交线段 BC 于点 E,过点 E 作 EF⊥PE 交抛物线于点 F,连接 FB,FC,求△BCF 的面积的最大值;② 连接 PB,求35PC+PB 的最小值.图 K13-3【参考答案】1.解:(1)将 A(-1,0),B(3,0)的坐标代入 y=ax2+bx+6,得:{a-b+6=0,9a+3b+6=0,解得{a=-2,b=4 , ∴抛物线的解析式为 y=-2x2+4x+6.(2)过点 P 作 PF∥y 轴,交 BC 于点 F,如图所示.当 x=0 时,y=-2x2+4x+6=6,∴点 C 的坐标为(0,6).设直线 BC 的解析式为 y=kx+c,将 B(3,0),C(0,6)的坐标代入 y=kx+c,得:{3k+c=0,c=6,解得:{k=-2,c=6,∴直线 BC 的解析式为 y=-2x+6.由题意,n=-2m2+4m+6,∴点 P 的坐标为(m,-2m2+4m+6),则点 F 的坐标为(m,-2m+6),∴PF=-2m2+4m+6-(-2m+6)=-2m2+6m,∴△PBC 的面积 S=12PF·OB=-3m2+9m=-3 m-322+274 (0