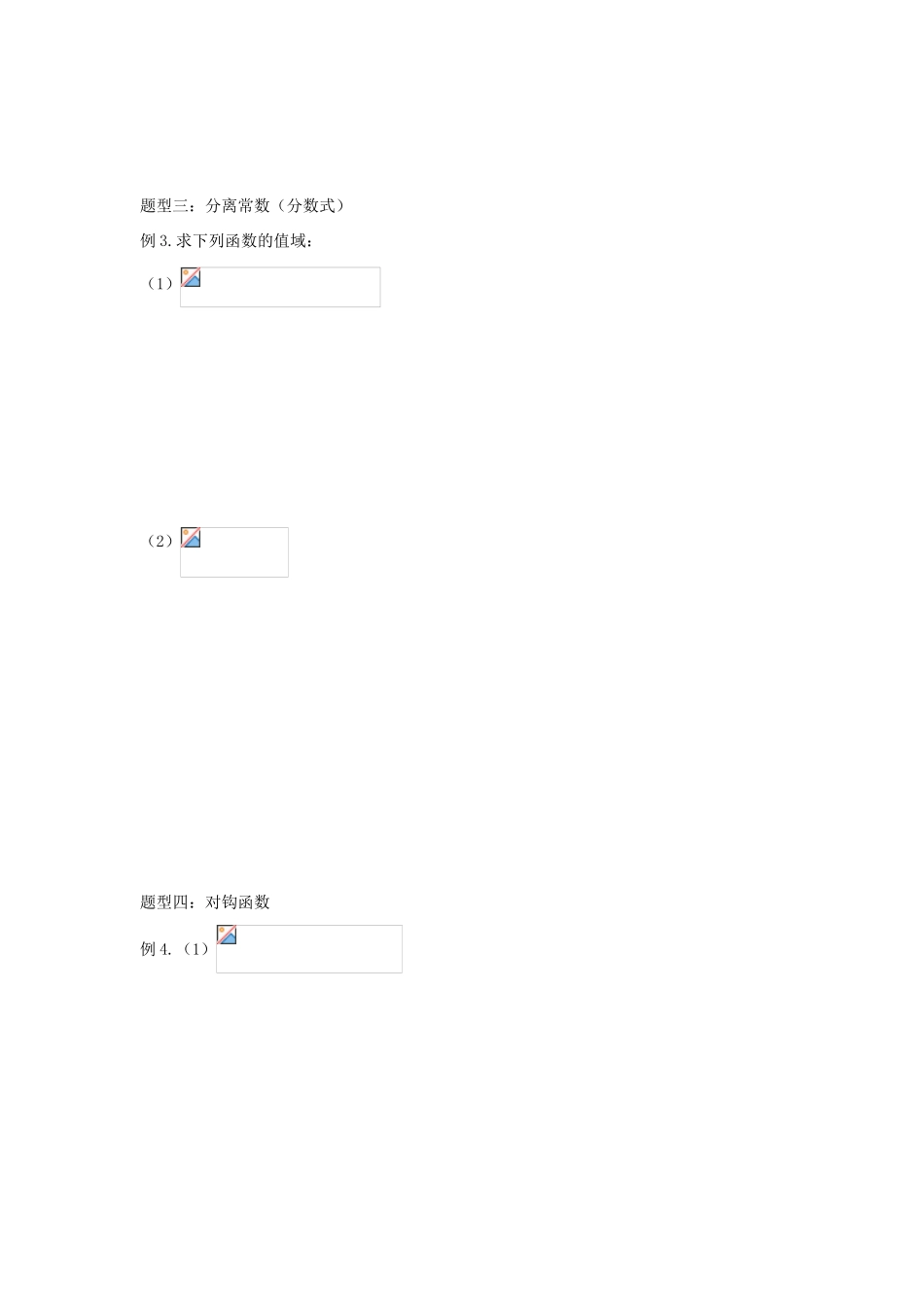
河北省衡水中学高一数学必修一学案:1.3.1 函数的最值(第三课时)方法汇总:1. 函数值域是函数的三要素之一,它由定义域和对应法则两要素唯一确定,由于函数的值域是函数值的集合,因此,函数的值域必须用集合或区间表示。 2。求函数的值域没有通行通 法,只能依据函数解析式的结构特征确定相应的解法,常用方法有:⑴ 与二次函数有关的函数,可用配方法(注意定义域)⑵ 形如的形式,可用换元法。即令,转化成二次函数求值域(注意t 的取值范围)⑶ 形如型的函数可借助反比例函数,求其值域。这种函数的值域是⑷ 单调性法:确定函数的定义域(或定义域上的子集上)的单调 性求出函数值域的方法。形如(a,b,c,d 均为常数,且),看 a,c 是否同号,若同号用单调性求值域;若异号则用换元法求值域.⑸ 函数,当时利用单调性结论,当利用对构函数求解。⑹ 数形结合法:利用函数的解析式求所表示的几何意义 (有时需要对解析式进行必要的变形),借助几何方法或图像求函数值域注意:因为函数的定义域 制约函数的值域,因此无论采取什么方法求值域,均应先考虑函数的定义域。思路方法:题型一:配方法:(二次函数在闭区间上 的最值问题)例 1.(1)求的值域;(2)求函数的值域;(3)求函数的值域。题型二:换元法:(转化为二次函数型)例 2.求下列函数的值域:(1);(2)(两种方法)。题型三:分离常数(分数式)例 3.求下列函数的值域:(1)(2)题型四:对钩函数例 4.(1)(2)求函数在区间上的最大值和最小值。题型五:数形结合:例 5.求下列函数的值域课堂小结: