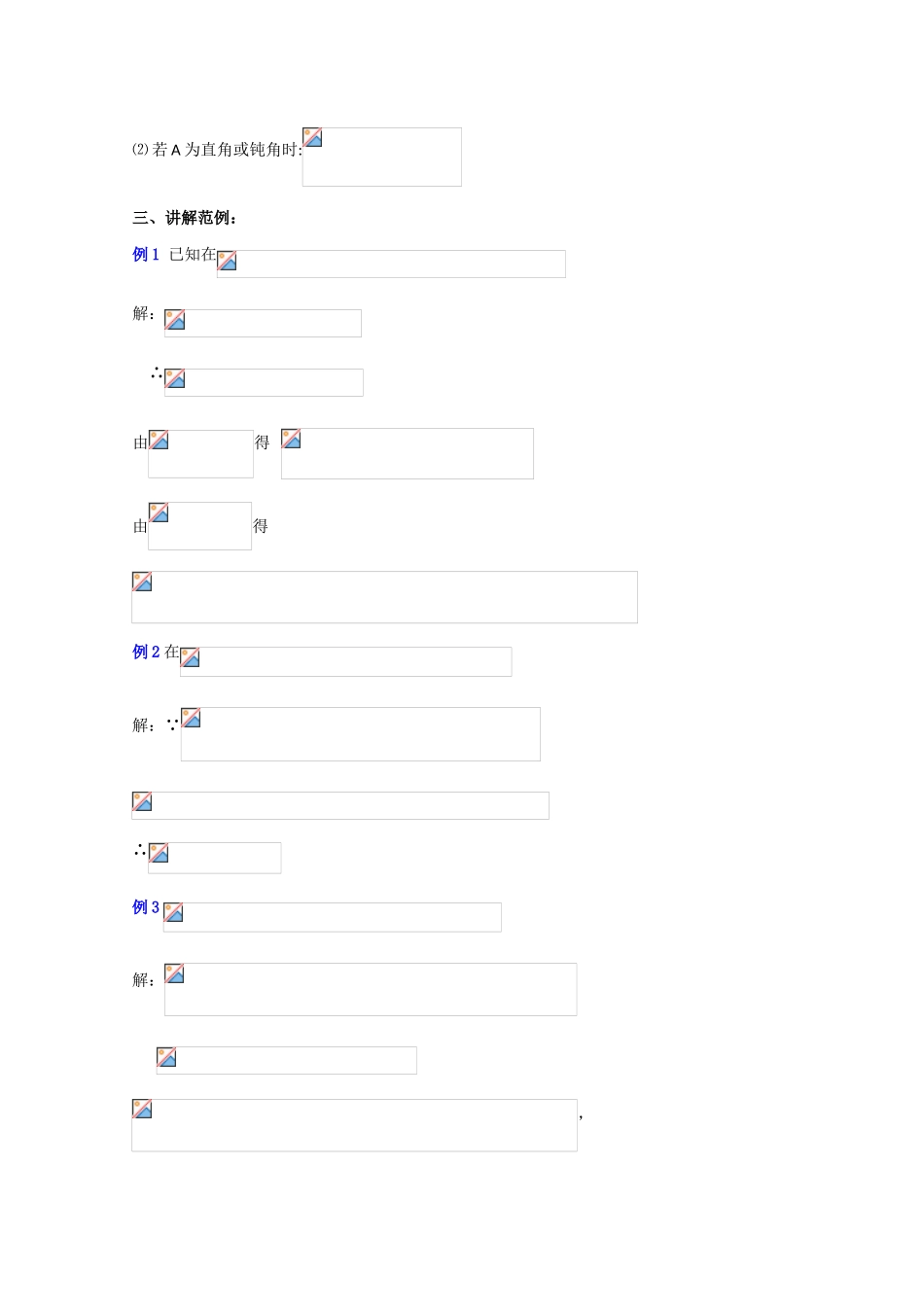
课 题:正弦定理、余弦定理(1)教学目的:⑴ 使学生掌握正弦定理⑵ 能应用解斜三角形,解决实际问题教学重点:正弦定理教学难点:正弦定理的正确理解和熟练运用授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪教学过程:一、引言:在直角三角形中,由三角形内角和定理、勾股定理、锐角三角函数,可以由已知的边和角求出未知的边和角那么斜三角形怎么办?——提出课题:正弦定理、余弦定理 二、讲解新课:正弦定理:在任一个三角形中,各边和它所对角的正弦比相等,即 == =2R(R 为△ABC 外接圆半径) 1.直角三角形中:sinA= ,sinB=, sinC=1 即 c=, c= , c=. ∴==2.斜三角形中 证明一:(等积法)在任意斜△ABC 当中S△ABC= 两边同除以即得:==证明二:(外接圆法)如图所示,∠A=∠D∴同理 =2R,=2R证明三:(向量法)过 A 作单位向量垂直于由 += 两边同乘以单位向量 得 •(+)=•则•+•=•∴||•||cos90+||•||cos(90C)=||•||cos(90A)∴ ∴=同理,若过 C 作垂直于得: = ∴==正弦定理的应用 从理论上正弦定理可解决两类问题: 1.两角和任意一边,求其它两边和一角;2.两边和其中一边对角,求另一边的对角,进而可求其它的边和角(见图示)已知 a, b 和 A, 用正弦定理求 B 时的各种情况:⑴ 若 A 为锐角时:babababaa已知边a,b和A仅有一个解有两个解仅有一个解无解abCH=bsinA