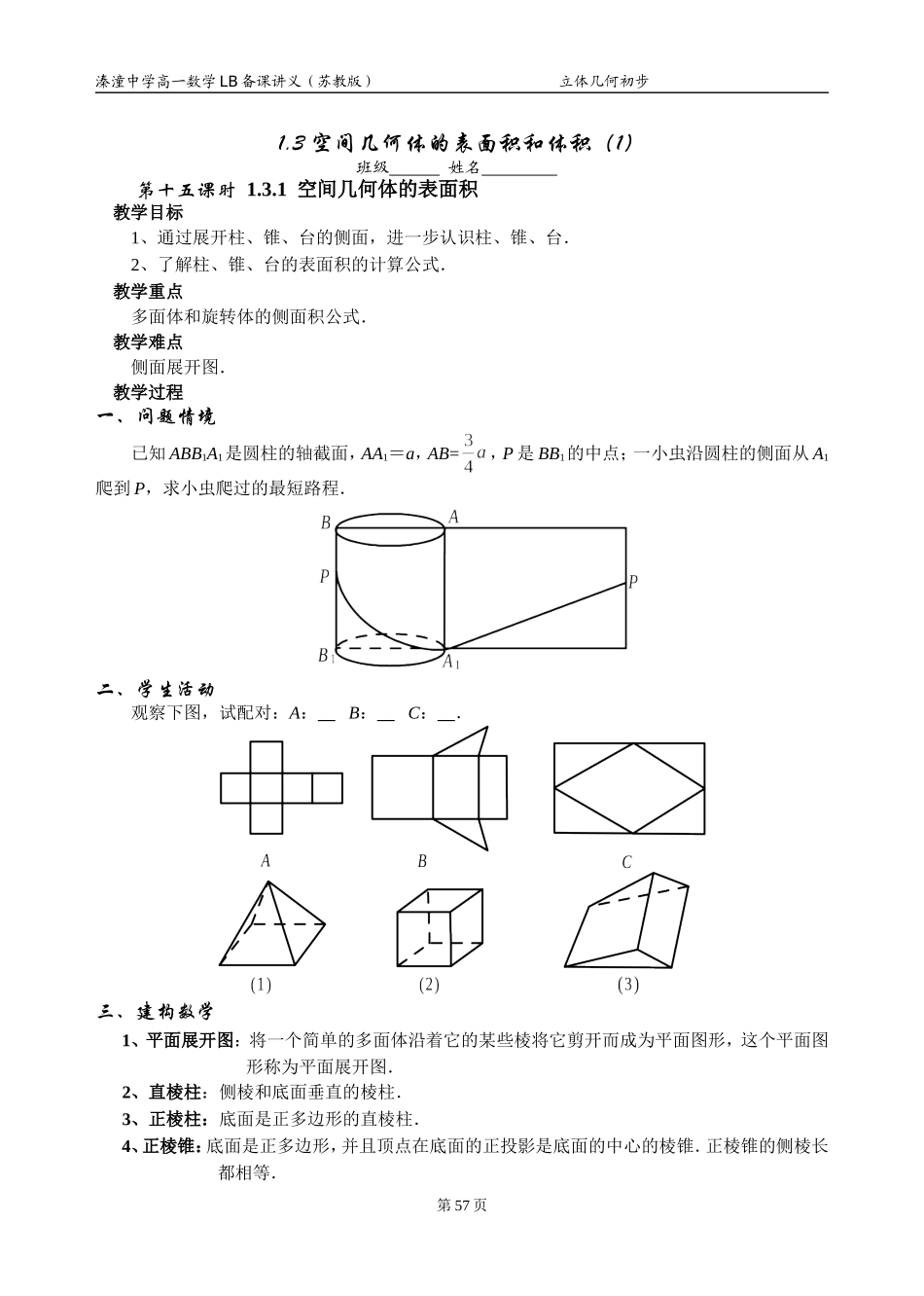
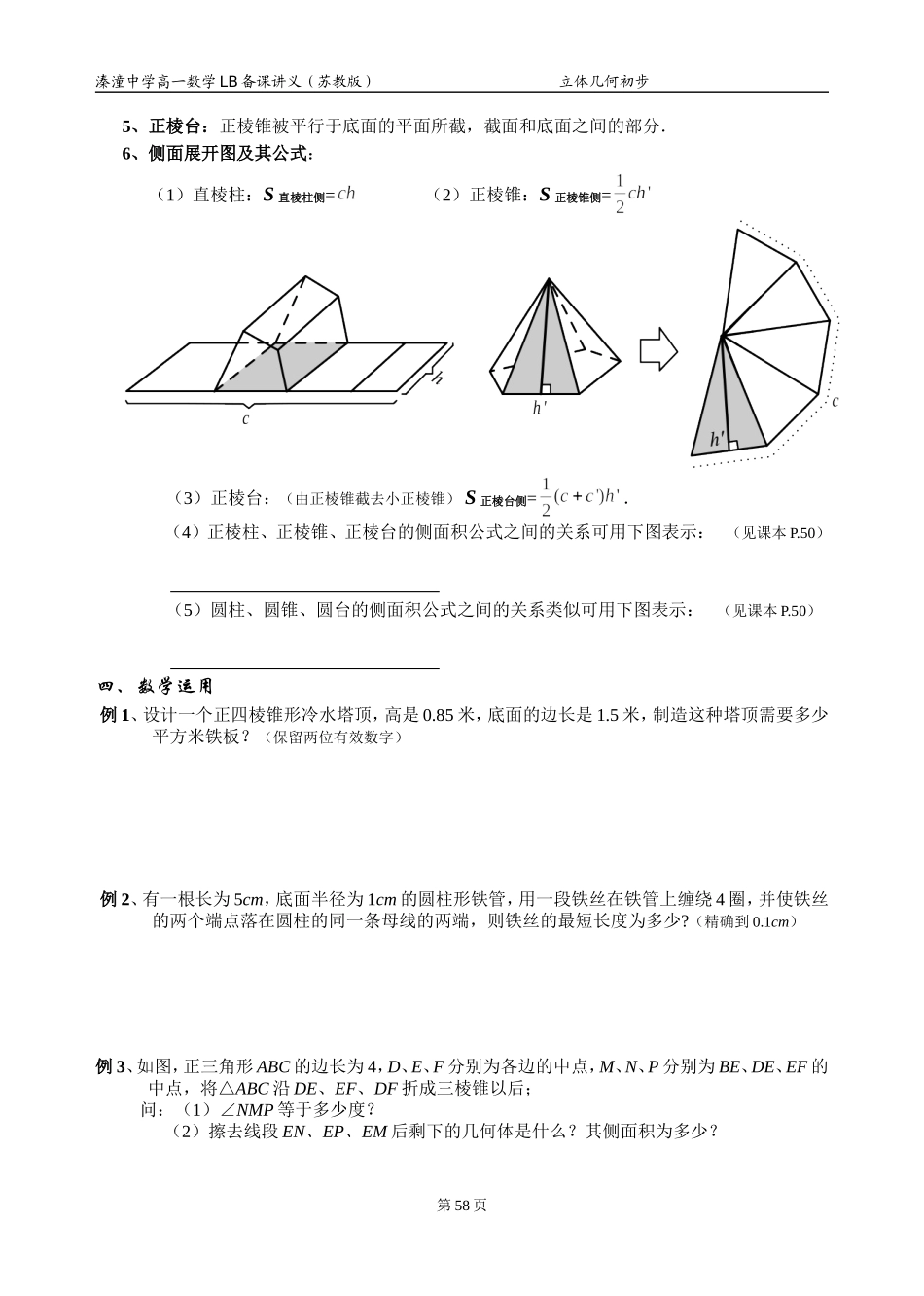
溱潼中学高一数学 LB 备课讲义(苏教版) 立体几何初步1.3 空间几何体的表面积和体积(1) 班级 姓名 第十五课时 1.3.1 空间几何体的表面积教学目标1、通过展开柱、锥、台的侧面,进一步认识柱、锥、台.2、了解柱、锥、台的表面积的计算公式.教学重点多面体和旋转体的侧面积公式.教学难点侧面展开图.教学过程一、问题情境已知 ABB1A1是圆柱的轴截面,AA1=a,AB=,P 是 BB1的中点;一小虫沿圆柱的侧面从 A1爬到 P,求小虫爬过的最短路程.二、学生活动观察下图,试配对:A: B: C: .三、建构数学1、平面展开图:将一个简单的多面体沿着它的某些棱将它剪开而成为平面图形,这个平面图形称为平面展开图.2、直棱柱:侧棱和底面垂直的棱柱.3、正棱柱:底面是正多边形的直棱柱.4、正棱锥:底面是正多边形,并且顶点在底面的正投影是底面的中心的棱锥.正棱锥的侧棱长都相等.第 57 页溱潼中学高一数学 LB 备课讲义(苏教版) 立体几何初步5、正棱台:正棱锥被平行于底面的平面所截,截面和底面之间的部分.6、侧面展开图及其公式:(1)直棱柱:S 直棱柱侧= (2)正棱锥:S 正棱锥侧=(3)正棱台:(由正棱锥截去小正棱锥) S 正棱台侧=.(4)正棱柱、正棱锥、正棱台的侧面积公式之间的关系可用下图表示: (见课本 P.50) (5)圆柱、圆锥、圆台的侧面积公式之间的关系类似可用下图表示:(见课本 P.50) 四、数学运用例 1、设计一个正四棱锥形冷水塔顶,高是 0.85 米,底面的边长是 1.5 米,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)例 2、有一根长为 5cm,底面半径为 1cm 的圆柱形铁管,用一段铁丝在铁管上缠绕 4 圈,并使铁丝的两个端点落在圆柱的同一条母线的两端,则铁丝的最短长度为多少?(精确到 0.1cm)例 3、如图,正三角形 ABC 的边长为 4,D、E、F 分别为各边的中点,M、N、P 分别为 BE、DE、EF 的中点,将△ABC 沿 DE、EF、DF 折成三棱锥以后;问:(1)∠NMP 等于多少度?(2)擦去线段 EN、EP、EM 后剩下的几何体是什么?其侧面积为多少?第 58 页溱潼中学高一数学 LB 备课讲义(苏教版) 立体几何初步例 4、已知圆锥有一个内接圆柱,此圆柱的底面在圆锥的底面上,圆柱的高等于圆锥的底面半径,且圆柱的全面积∶圆锥的底面积=3∶2;(1)求圆锥母线与底面所成的角的正切值;(2)圆锥的侧面积与圆柱的侧面积的比.学生练习:课本 P.53 1、2...