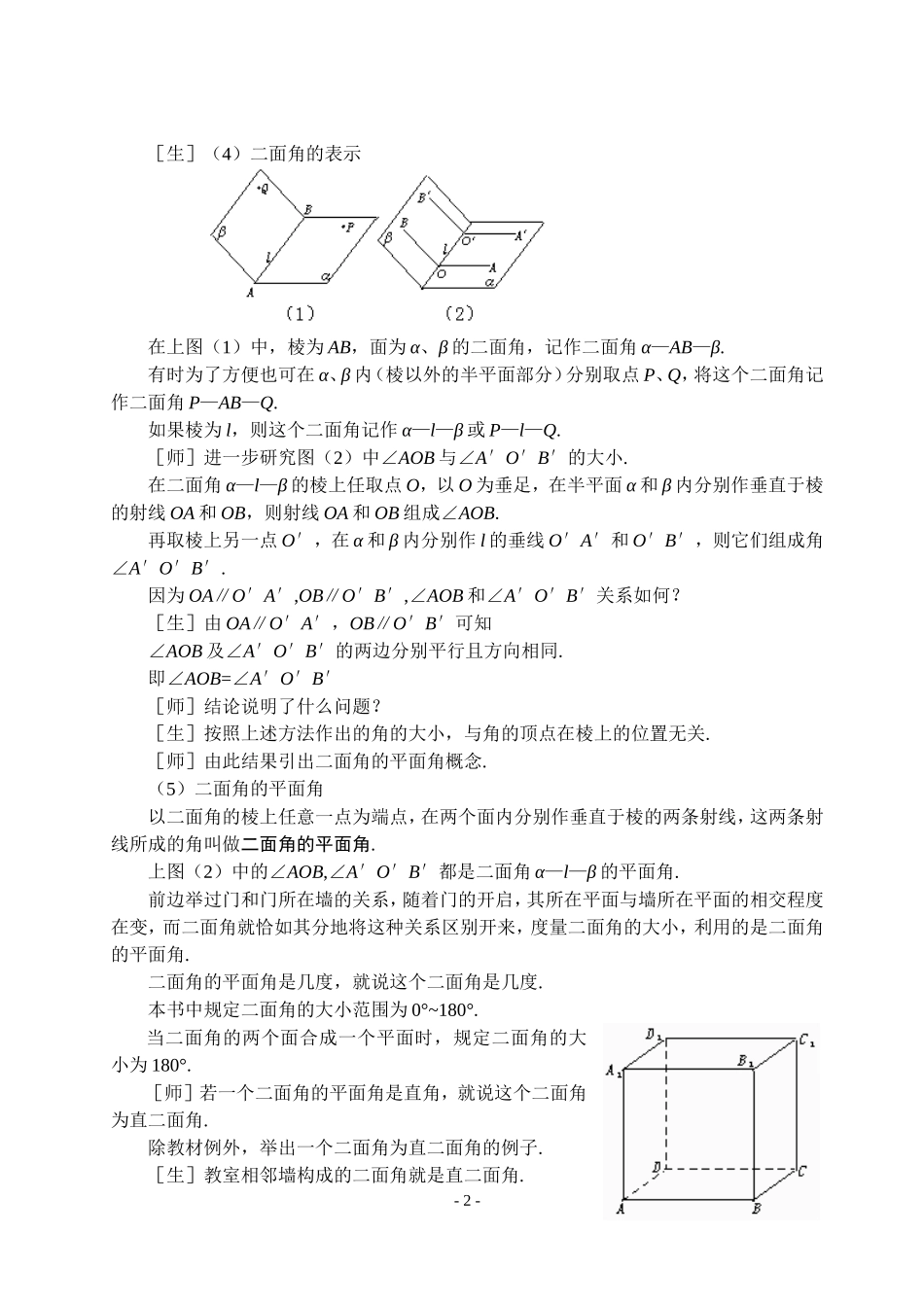
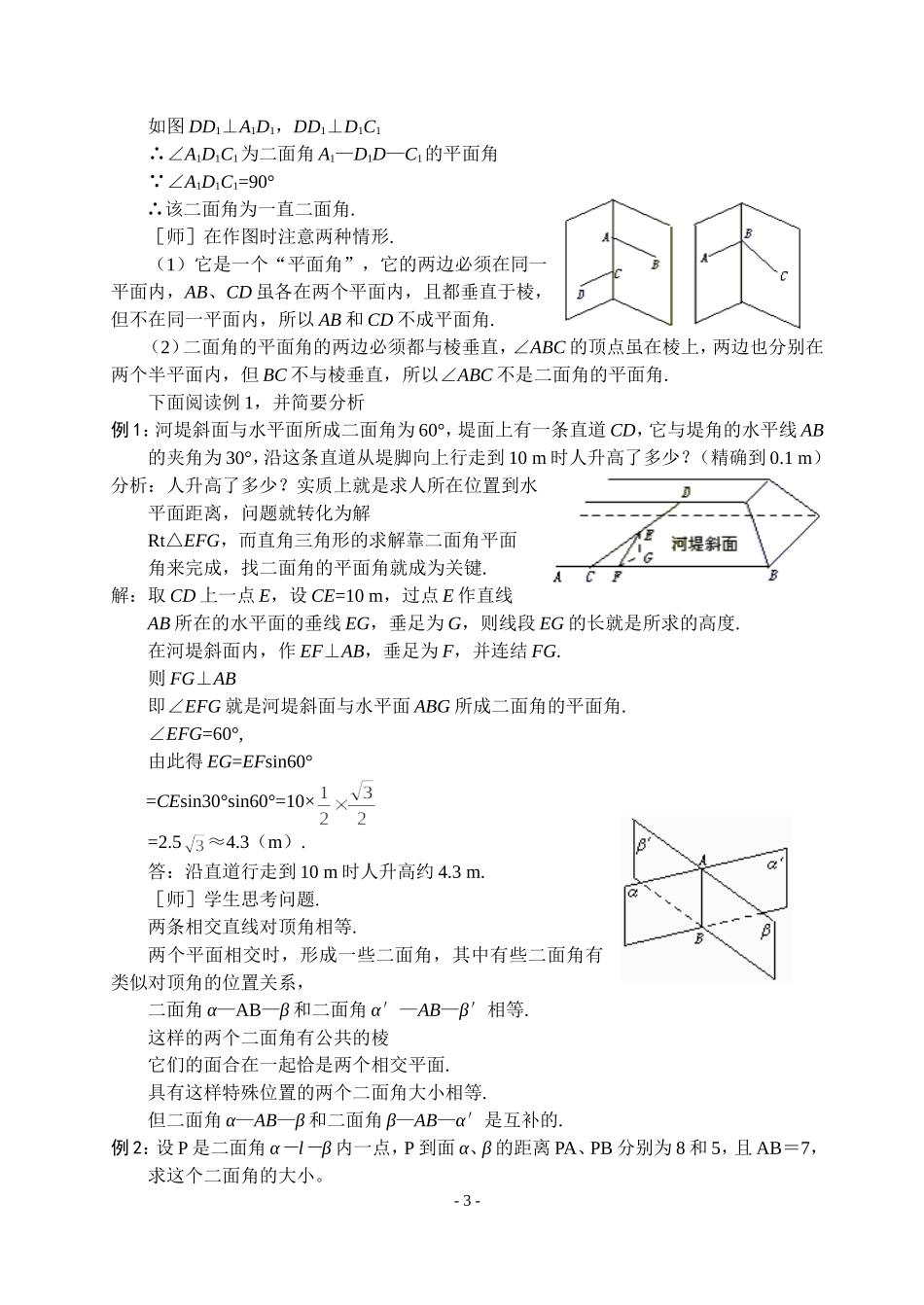
1.2.4 平面与平面的位置关系(第 2 课时) 二 面 角教学目标:使学生正确理解二面角及二面角的平面角;通过概念教学,提高逻辑思维能力,渗透等价转化思想;通过图形结构分析,掌握作图方法,提高空间想象能力;通过本节教学由水坝、卫星运行轨道平面到二面角,体现由具体到抽象思想。教学重点:二面角的平面角。教学难点: 求作二面角的平面角。教学过程:1.复习回顾:两个平面平行的判定有哪几种方法?各种方法应具备条件是什么?两个平面平行的性质有哪些?如何利用性质解决问题?这一部分中等价转化思想体现在哪里?2.讲授新课:1.二面角[师]两个平面的位置关系包括相交、平行两种,两个平行平面的相对位置是用“距离”来刻画.而两个相交平面的相对位置由这两个平面所成的“角”来确定.修筑水坝,为了使水坝坚固耐久,必须使水坝面和水平面成适当的角度(如图)。还有教材中人造地球卫星的发射,需卫星轨道平面和地球赤道平面成一定的角度.请同学们再举出生活中例子说明结论.那就是:为了解决实际问题,需研究两个平面所成的角.[师]请同学归纳总结二面角的概念.(可与平面角概念对比)二面角的概念(1)半平面的定义:平面内的一条直线,把这个平面分成两部分,其中的每一部分都叫做半平面.(2)二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫二面角的棱,这两个半平面叫二面角的面.[师](3)常用直立式和平卧式两种(教师和学生共同动手)直立式: 平卧式:- 1 -[生](4)二面角的表示在上图(1)中,棱为 AB,面为 α、β 的二面角,记作二面角 α—AB—β.有时为了方便也可在 α、β 内(棱以外的半平面部分)分别取点 P、Q,将这个二面角记作二面角 P—AB—Q.如果棱为 l,则这个二面角记作 α—l—β 或 P—l—Q.[师]进一步研究图(2)中∠AOB 与∠A′O′B′的大小.在二面角 α—l—β 的棱上任取点 O,以 O 为垂足,在半平面 α 和 β 内分别作垂直于棱的射线 OA 和 OB,则射线 OA 和 OB 组成∠AOB.再取棱上另一点 O′,在 α 和 β 内分别作 l 的垂线 O′A′和 O′B′,则它们组成角∠A′O′B′.因为 OA∥O′A′,OB∥O′B′,∠AOB 和∠A′O′B′关系如何?[生]由 OA∥O′A′,OB∥O′B′可知∠AOB 及∠A′O′B′的两边分别平行且方向相同.即∠AOB=∠A′O′B′[师]结论说明了什么问题?[生]按照上述方法作出的角的大小,与角的顶...