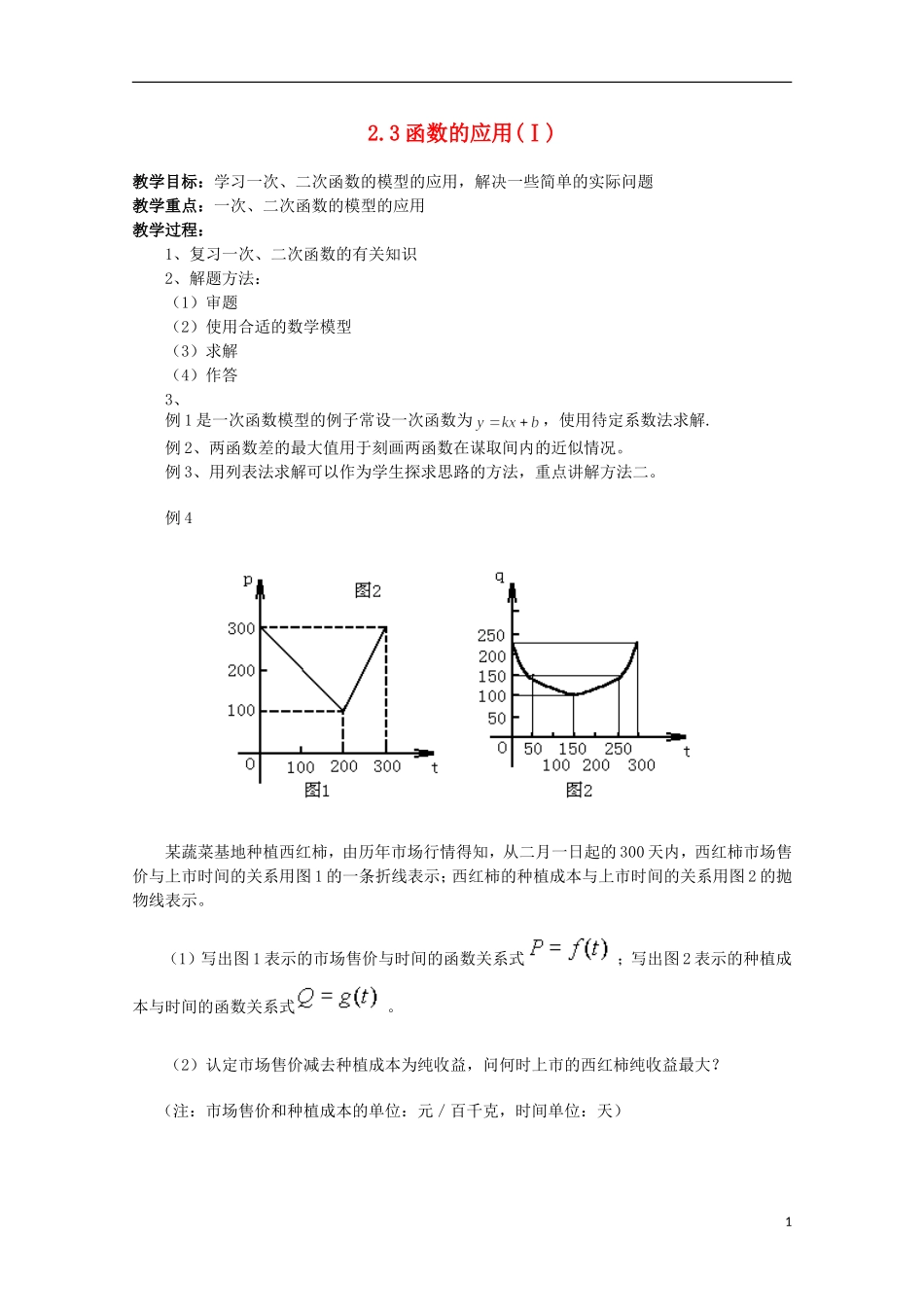
2.3 函数的应用(Ⅰ)教学目标:学习一次、二次函数的模型的应用,解决一些简单的实际问题教学重点:一次、二次函数的模型的应用教学过程:1、复习一次、二次函数的有关知识2、解题方法:(1)审题(2)使用合适的数学模型(3)求解(4)作答3、例 1 是一次函数模型的例子常设一次函数为,使用待定系数法求解.例 2、两函数差的最大值用于刻画两函数在谋取间内的近似情况。例 3、用列表法求解可以作为学生探求思路的方法,重点讲解方法二。例 4某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的 300 天内,西红柿市场售价与上市时间的关系用图 1 的一条折线表示;西红柿的种植成本与上市时间的关系用图 2 的抛物线表示。(1)写出图 1 表示的市场售价与时间的函数关系式;写出图 2 表示的种植成本与时间的函数关系式。(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大? (注:市场售价和种植成本的单位:元/百千克,时间单位:天)1杰: 由图 1 可得市场售价与时间 t 的函数关系:,由图 2 可得种植成本与时间 t 的函数关系:,由上消去 t 得 Q 与 P 的对应关系式:。 因为认定市场售价 P 与种植成本 Q 之差为纯收益,所以当且时,;由二次函数性质可知当 P=250 时,t=50,此时 P-Q 取得最大值 100; 当且时,;由二次函数性质可知当 P=300 时,t=300,此时P-Q 取得最大值 87.5。因为 100>87.5,所以当 t=50 时,P-Q 取得最大值 100,即从二月一日起的第 50 天上市的西红柿收益最大。课堂练习:第 73 页习题 2-3A小结:本节课学习了一次、二次函数的模型的应用,解决一些简单的实际问题课后作业:第 73 页习题 2-3B,1,3,42