2007年江苏省常州市第八中学高一数学函数的单调性教学设计 苏教版

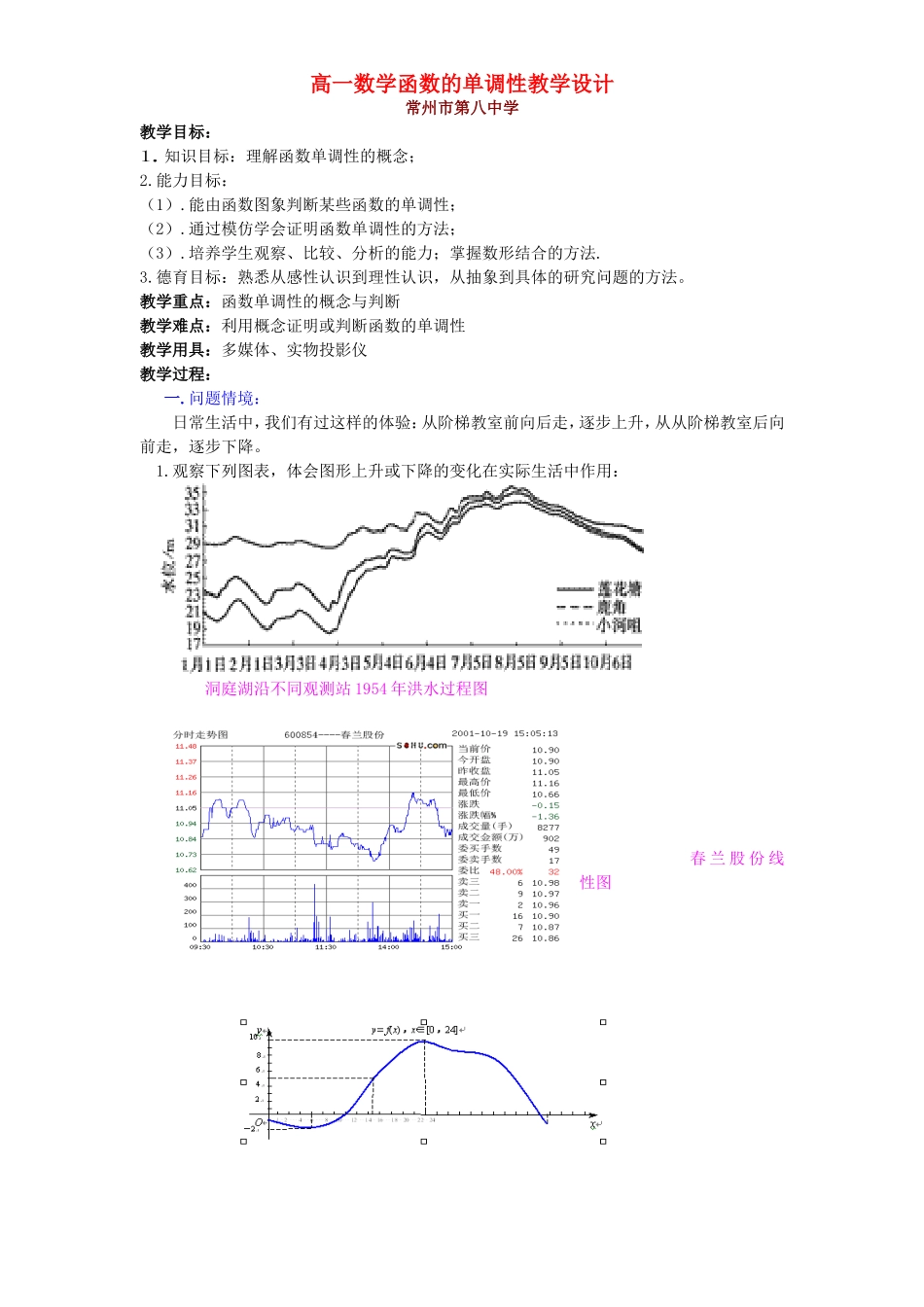
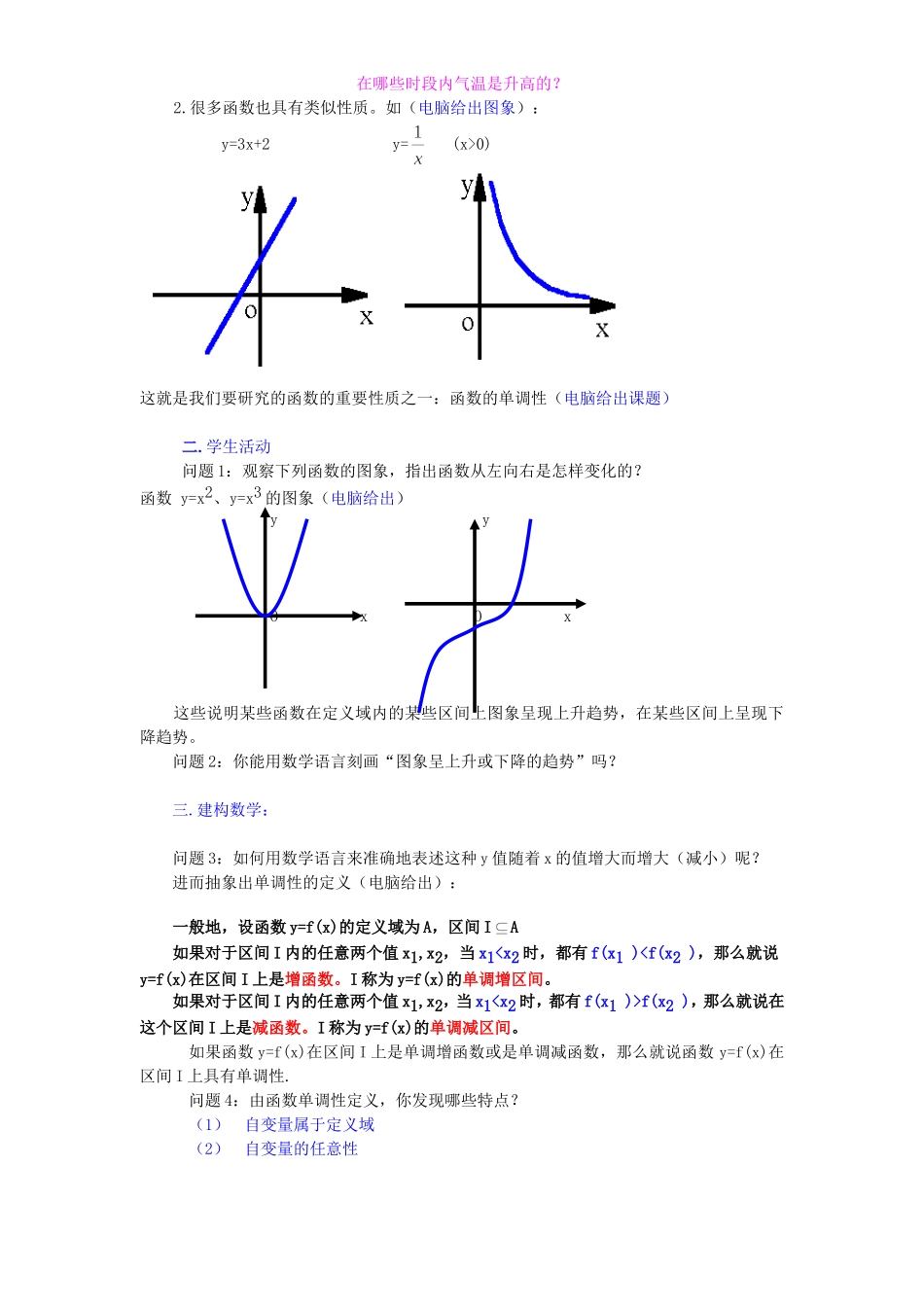
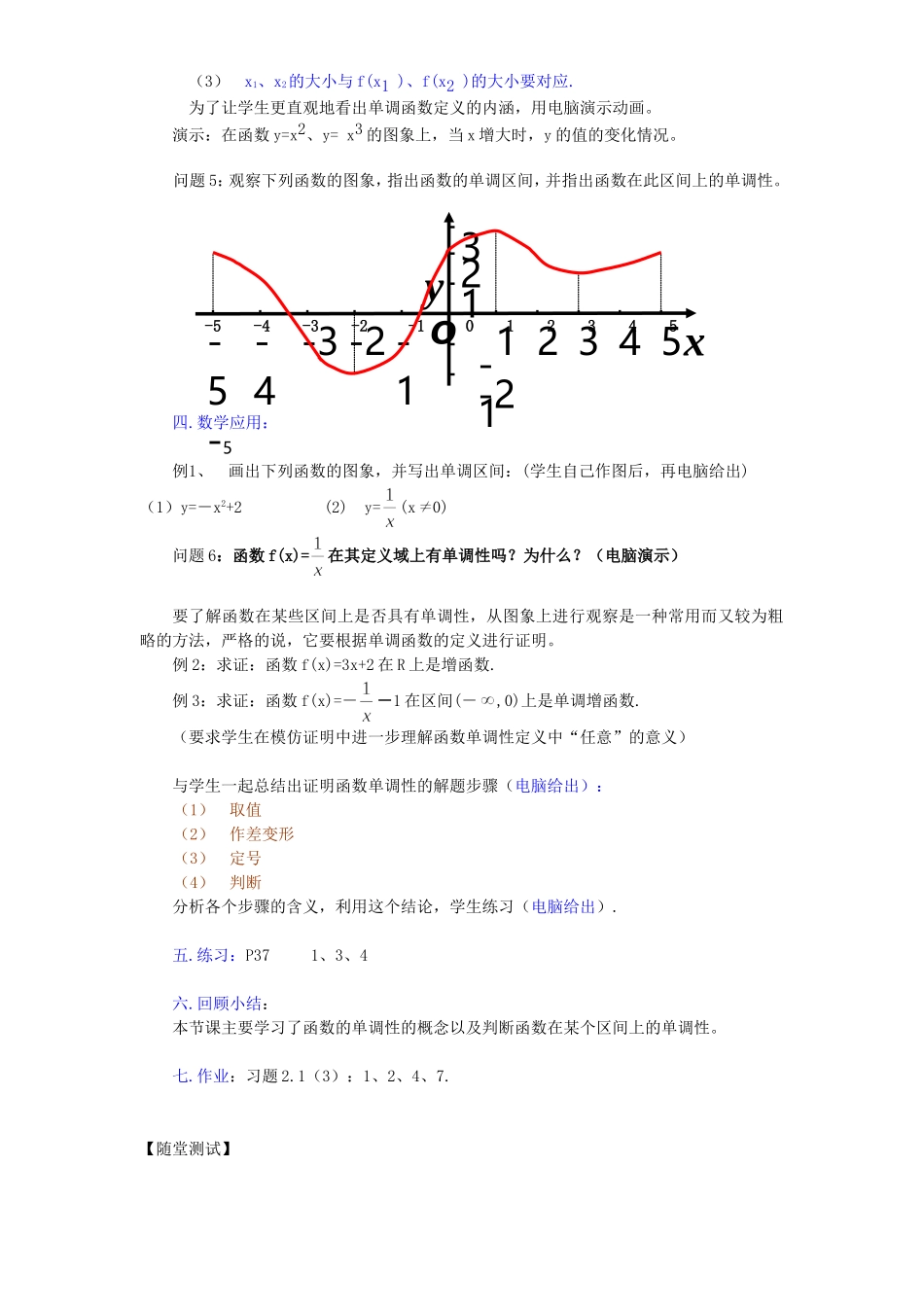
高一数学函数的单调性教学设计常州市第八中学教学目标：1.知识目标：理解函数单调性的概念；2.能力目标：（1）.能由函数图象判断某些函数的单调性；（2）.通过模仿学会证明函数单调性的方法；（3）.培养学生观察、比较、分析的能力；掌握数形结合的方法.3.德育目标：熟悉从感性认识到理性认识，从抽象到具体的研究问题的方法。教学重点：函数单调性的概念与判断教学难点：利用概念证明或判断函数的单调性教学用具：多媒体、实物投影仪教学过程：一.问题情境： 日常生活中，我们有过这样的体验：从阶梯教室前向后走，逐步上升，从从阶梯教室后向前走，逐步下降。1.观察下列图表，体会图形上升或下降的变化在实际生活中作用：洞庭湖沿不同观测站 1954 年洪水过程图春 兰 股 份 线性图在哪些时段内气温是升高的？2.很多函数也具有类似性质。如（电脑给出图象）：y=3x+2 y= (x>0)这就是我们要研究的函数的重要性质之一：函数的单调性（电脑给出课题）二.学生活动问题 1：观察下列函数的图象，指出函数从左向右是怎样变化的？函数 y=x2、y=x3 的图象（电脑给出） y y O x O x 这些说明某些函数在定义域内的某些区间上图象呈现上升趋势，在某些区间上呈现下降趋势。 问题 2：你能用数学语言刻画“图象呈上升或下降的趋势”吗？三.建构数学：问题 3：如何用数学语言来准确地表述这种 y 值随着 x 的值增大而增大（减小）呢？进而抽象出单调性的定义（电脑给出）：一般地，设函数 y=f(x)的定义域为 A，区间 IA如果对于区间 I 内的任意两个值 x1,x2，当 x1f(x2 )，那么就说在这个区间 I 上是减函数。I 称为 y=f(x)的单调减区间。如果函数 y=f(x)在区间 I 上是单调增函数或是单调减函数，那么就说函数 y=f(x)在区间 I 上具有单调性.问题 4：由函数单调性定义，你发现哪些特点？（1）自变量属于定义域（2）自变量的任意性（3）x1、x2的大小与 f(x1 )、f(x2 )的大小要对应.为了让学生更直观地看出单调函数定义的内涵，用电脑演示动画。演示：在函数 y=x2、y= x3 的图象上，当 x 增大时，y 的值的变化情况。问题 5：观察下列函数的图象，指出函数的单调区间，并指出函数在此区间上的单调性。 -5 -4 -3 -2 -1 0 1 2 ...