2010届高考数学第一轮复习精品教案：第七、八章 平面解析几何

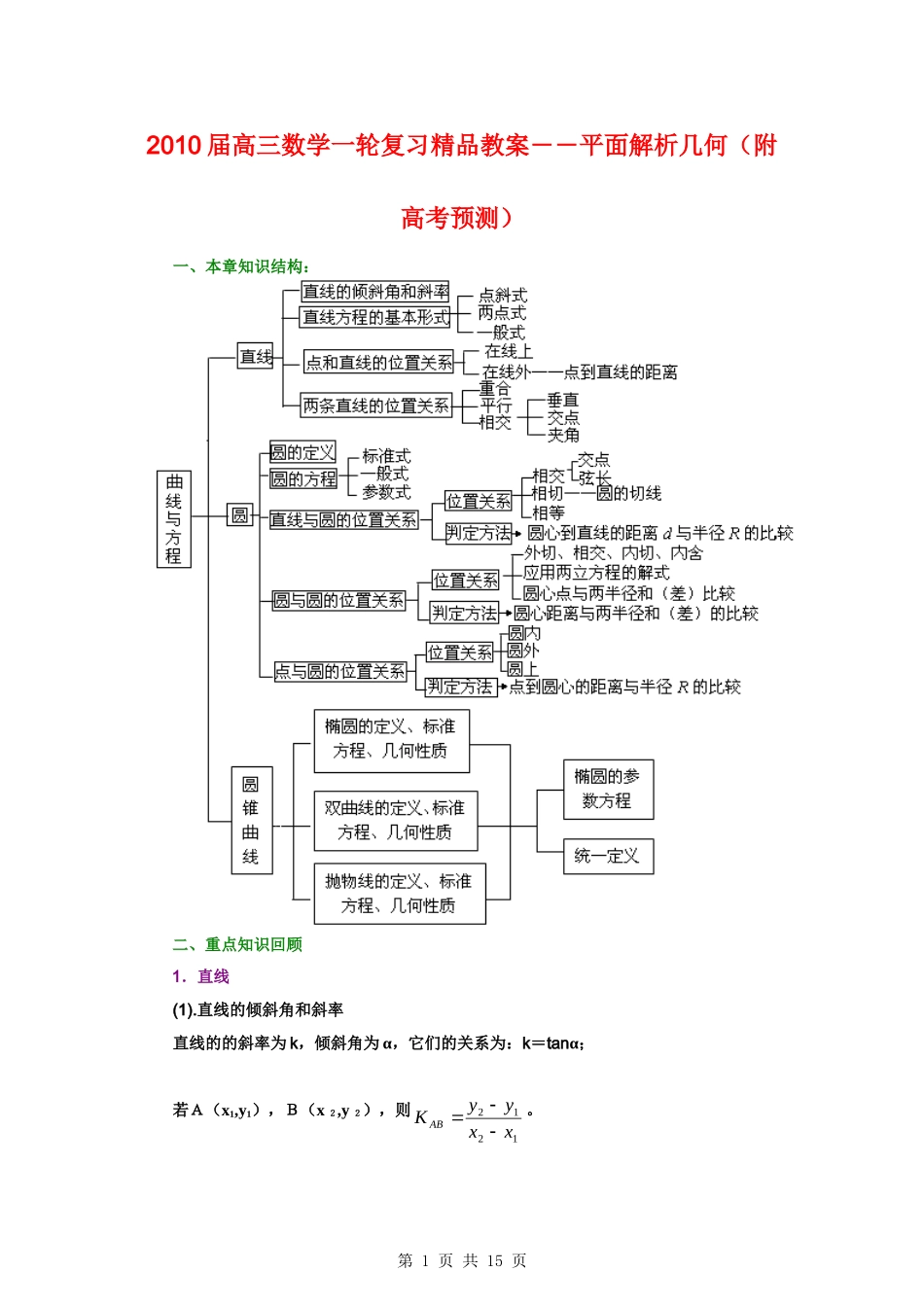
2010 届高三数学一轮复习精品教案――平面解析几何（附高考预测）一、本章知识结构：二、重点知识回顾1．直线(1).直线的倾斜角和斜率 直线的的斜率为 k，倾斜角为 α，它们的关系为：k＝tanα；若Ａ（x1,y1），Ｂ（x ２,y ２），则1212xxyyK AB。第 1 页 共 15 页(2) .直线的方程a.点斜式：)(11xxkyy； b.斜截式：bkxy；c.两点式：121121xxxxyyyy； d.截距式：1 byax；e.一般式：0CByAx，其中 A、B 不同时为 0. (3).两直线的位置关系两条直线1l ，2l 有三种位置关系：平行（没有公共点）；相交（有且只有一个公共点）；重合（有无数个公共点）.在这三种位置关系中，我们重点研究平行与相交。若直线1l 、2l 的斜率分别为1k 、2k ，则1l ∥2l 1k ＝2k ，1l ⊥2l 1k ·2k ＝－１。（4）点、直线之间的距离点 A（x0，y0）到直线0CByAx的距离为：d=2200||BACByAx。两点之间的距离：|AB|=212212)()yyxx（2. 圆 （1）圆方程的三种形式 标准式：222)()(rbyax，其中点（a，b）为圆心，r>0，r 为半径，圆的标准方程中有三个待定系数，使用该方程的最大优点是可以方便地看出圆的圆心坐标与半径的大小． 一般式：022FEyDxyx，其中22ED，为圆心FED42122为半径，，圆的一般方程中也有三个待定系数，即 D、E、F．若已知条件中没有直接给出圆心的坐标（如题目为：已知一个圆经过三个点，求圆的方程），则往往使用圆的一般方程求圆方程． 参数式：以原点为圆心、r 为半径的圆的参数方程是sin,cosryrx（其中 θ 为参数）． 以（a，b）为圆心、r 为半径的圆的参数方程为sin,cosrbyrax（θ 为参数），θ 的几何意义是：以垂直于 y 轴的直线与圆的右交点 A 与圆心 C 的连线为始边、以 C 与动点 P 的连线为终边的旋转角，如图所示．第 2 页 共 15 页 三种形式的方程可以相互转化，其流程图为： 2．二元二次方程是圆方程的充要条件 “A=C≠0 且 B=0”是一个一般的二元二次方程022FEyDxCyBxyAx表示圆的必要条件． 二 元 二 次 方 程022FEyDxCyBxyAx表 示 圆 的 充 要 条 件 为“A=C≠0、B=0 且0422AFED”，它可根据圆的一般方程推导而得． 3．参数方程与普通方程 我们现在所学的曲线方程有两大类，其一是普通方...