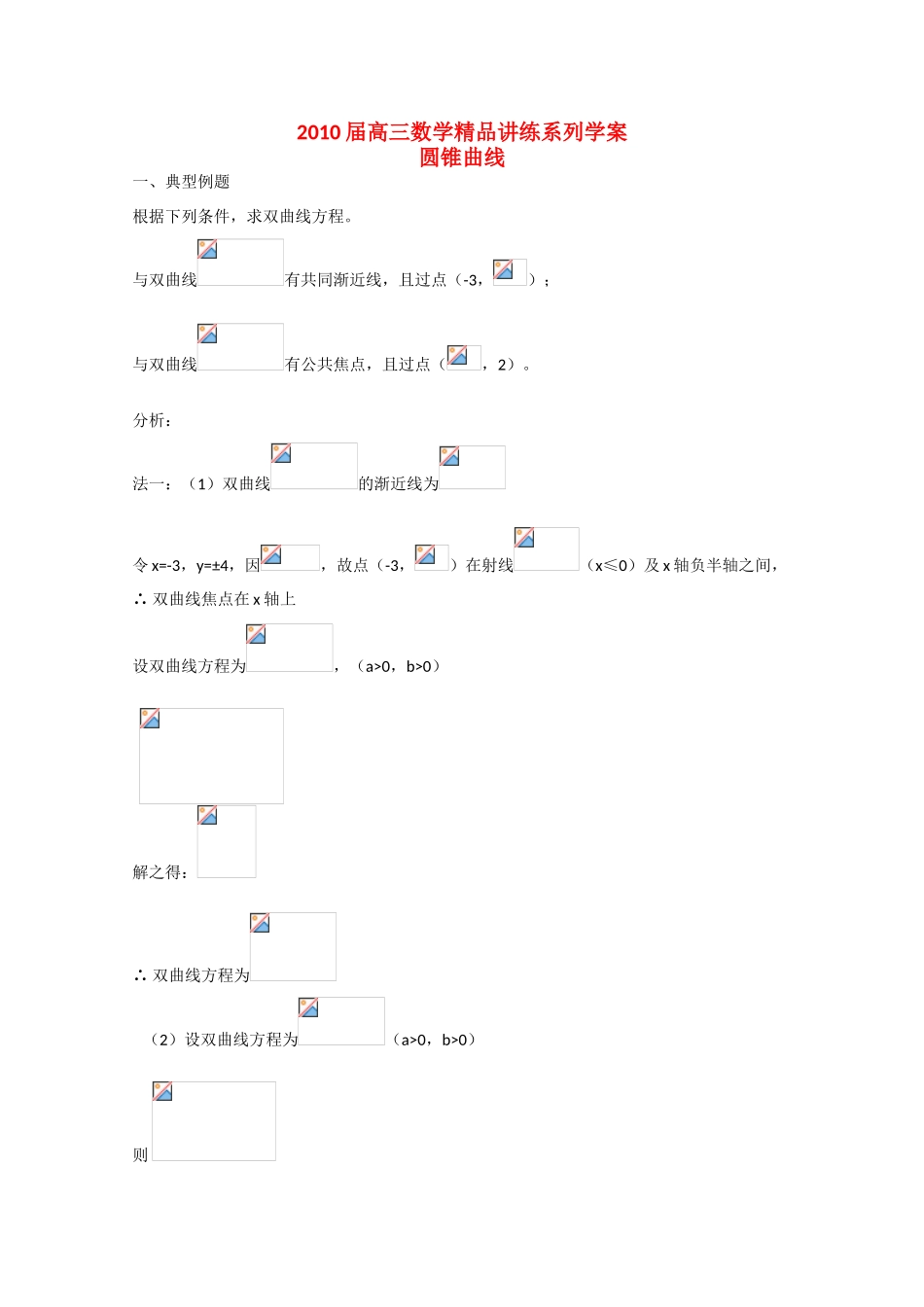
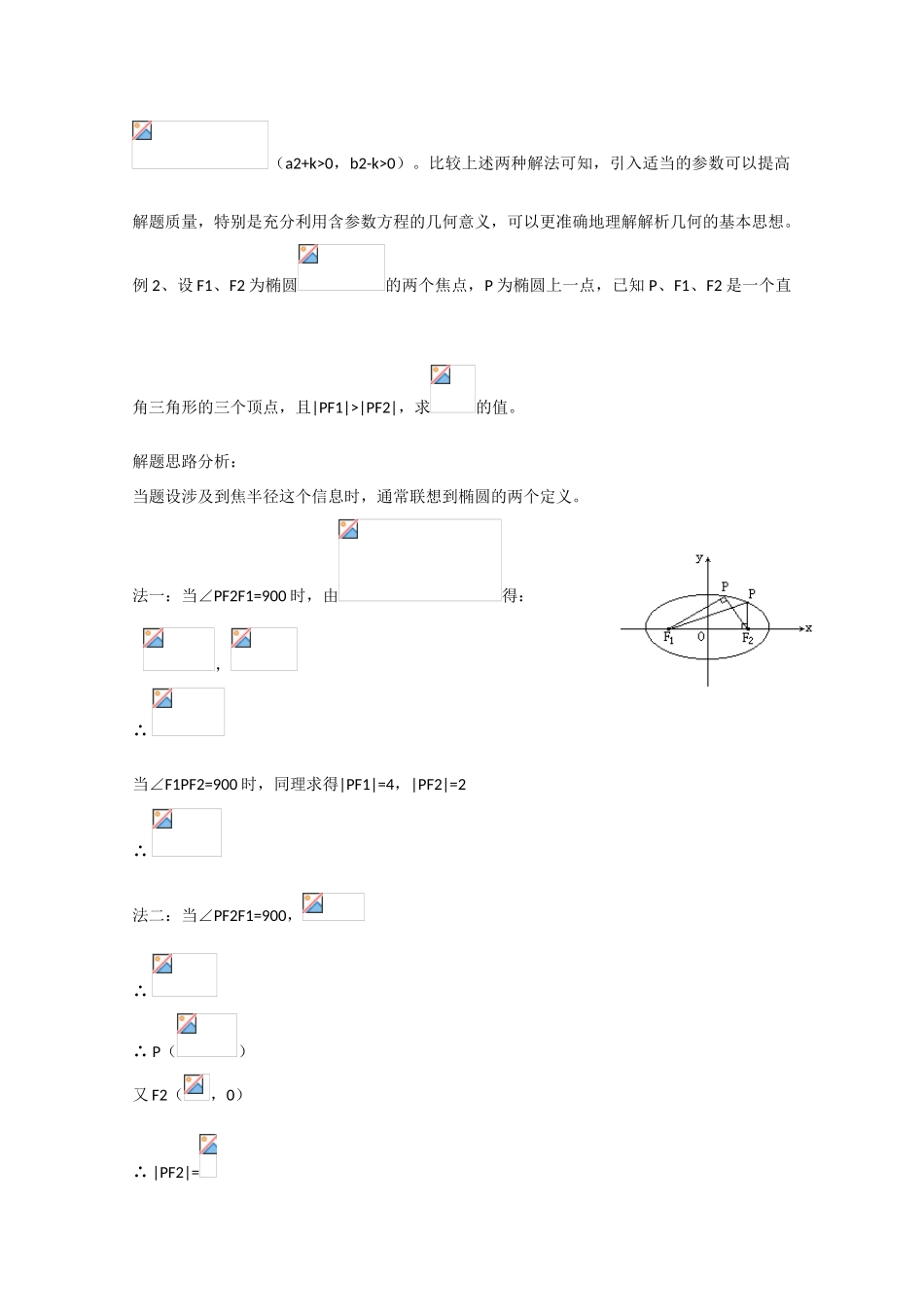
2010 届高三数学精品讲练系列学案圆锥曲线一、典型例题根据下列条件,求双曲线方程。与双曲线有共同渐近线,且过点(-3,);与双曲线有公共焦点,且过点(,2)。分析:法一:(1)双曲线的渐近线为令 x=-3,y=±4,因,故点(-3,)在射线(x≤0)及 x 轴负半轴之间,∴ 双曲线焦点在 x 轴上设双曲线方程为,(a>0,b>0) 解之得:∴ 双曲线方程为 (2)设双曲线方程为(a>0,b>0)则 解之得:∴ 双曲线方程为法二:(1)设双曲线方程为(λ≠0)∴ ∴ ∴ 双曲线方程为设双曲线方程为 ∴ 解之得:k=4∴ 双曲线方程为评注:与双曲线共渐近线的双曲线方程为(λ≠0),当 λ>0 时,焦点 在 x 轴 上 ; 当 λ<0 时 , 焦 点 在 y 轴 上 。 与 双 曲 线共 焦 点 的 双 曲 线 为(a2+k>0,b2-k>0)。比较上述两种解法可知,引入适当的参数可以提高解题质量,特别是充分利用含参数方程的几何意义,可以更准确地理解解析几何的基本思想。例 2、设 F1、F2 为椭圆的两个焦点,P 为椭圆上一点,已知 P、F1、F2 是一个直角三角形的三个顶点,且|PF1|>|PF2|,求的值。解题思路分析:当题设涉及到焦半径这个信息时,通常联想到椭圆的两个定义。法一:当∠PF2F1=900 时,由得: ,∴ 当∠F1PF2=900 时,同理求得|PF1|=4,|PF2|=2∴ 法二:当∠PF2F1=900,∴ ∴ P()又 F2(,0)∴ |PF2|=∴ |PF1|=2a-|PF2|=当∠F1PF2=900,由得: P()。下略。评注:由|PF1|>|PF2|的条件,直角顶点应有两种情况,需分类讨论。例 3、设点 P 到 M(-1,0),N(1,0)的距离之差为 2m,到 x 轴、y 轴的距离之比为 2,求m 取值范围。分析:根据题意,从点 P 的轨迹着手 ||PM|-|PN||=2m∴ 点 P 轨迹为双曲线,方程为(|m|<1) ①又 y=±2x(x≠0) ②①② 联立得:将此式看成是关于 x 的二次函数式,下求该二次函数值域,从而得到 m 的取值范围。根据双曲线有界性:|x|>m,x2>m2∴ 又 00∴ 且 m≠0∴ 评注:利用双曲线的定义找到点 P 轨迹是重要一步,当题目条件有等量关系时,一般考虑利用函数思想,建立函数关系式。例 4、已知 x2+y2=1,双曲线(x-1)2-y2=1,直线同时满足下列两个条件:①与双曲线交于不同两点;②与圆相切,且切点是直线与双曲线相交所得弦的中点。求直线方程。分析:选择适当的直线方程形式,把条件“是圆的切线”“切点 M 是弦...