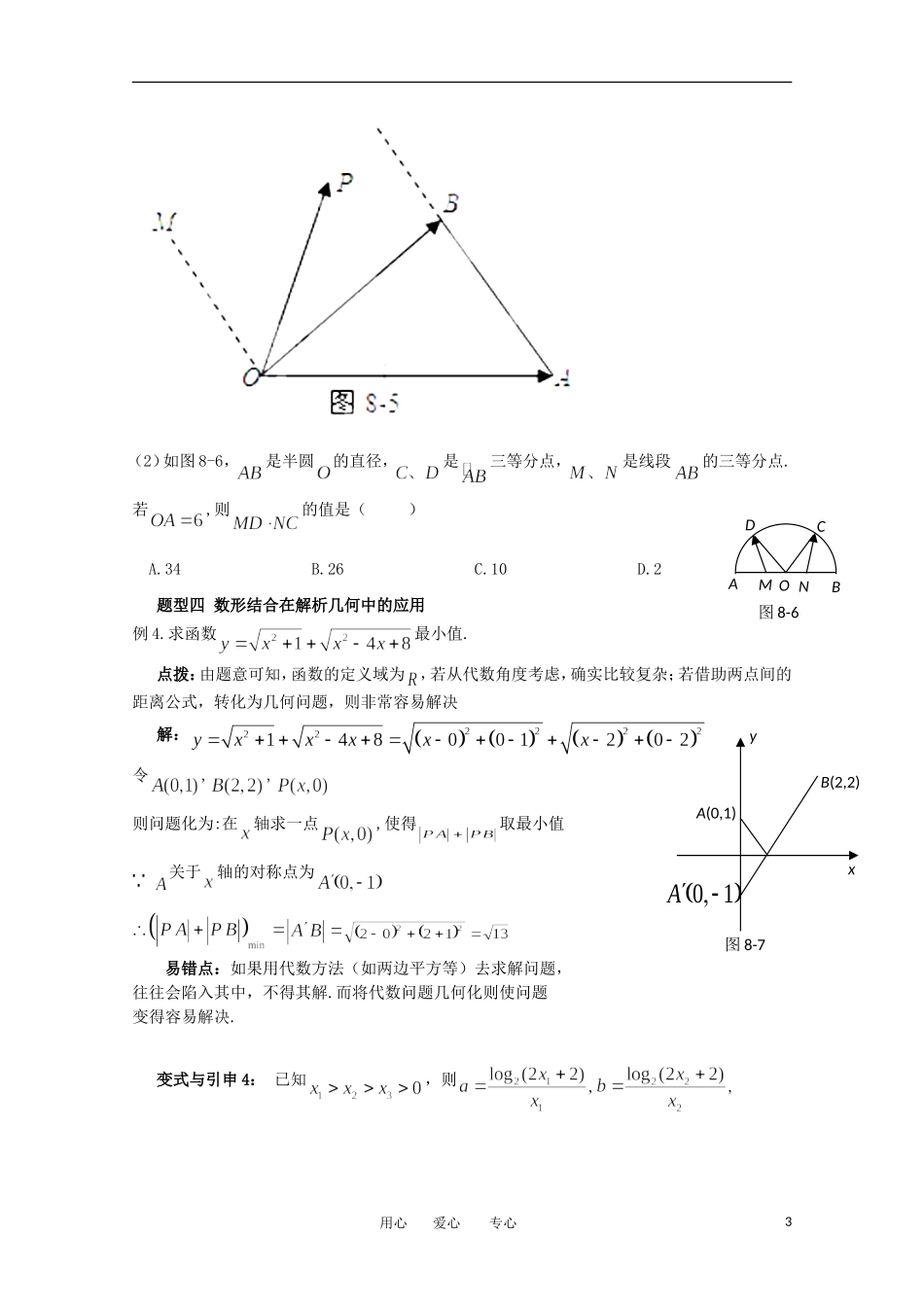
第二节 运用数形结合思想解题的策略数形结合思想通过“以形助数,以数解形”,使复杂问题简单化,抽象问题具体化,能够变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性与灵活性的有机结合.运用数形结合思想,不仅直观易发现解题途径,而且能避免复杂的计算与推理,大大简化了解题过程.这在解选择题、填空题中更显其优越.考试大纲的说明中强调:“在高考中,充分利用选择题和填空题的题型特点,为考查数形结合的思想提供了方便,能突出考查考生将复杂的数量关系转化为直观的几何图形问题来解决的意识,而在解答题中,考虑到推理论证的严密性,对数量关系问题的研究仍突出代数的方法而不提倡使用几何的方法,解答题中对数形结合思想的考查以由‘形’到‘数’的转化为主.”考试要求 展望 2011 年高考考查数形结合思法,可能会与以下内容为载体来命题:①函数与图象的对应关系;②曲线与方程的对应关系;③以几何元素和几何条件为背景建立起来的概念,如三角函数等;④所给的等式或代数式的结构含有明显的几何意义. 题型一 数形结合在函数与方程中的应用 例 1.已知且,试求使方程有解的实数 的取值范围.点拨:利用对数相等的意义,同时构造两个函数,通过函数的图象有没有交点进而得出方程有没有解,从而确定出 的取值范围. 解:原方程等价于构 造 曲 线, 直 线从 而 使 问 题 转 化 为 直 线和 双 曲 线() 在 轴上半部分有交点,求实数 的取值范围,如图 8-2 所示:有三条临界直线、、① 当 在和之间时,直线 在轴上的截距满足时, 与有一个交点,解之可得② 当 在上方时,直线 在轴上的截距满足时, 与有一个交点,解之可得综合①②可得,所求 的取值范围是 易错点: 解方程时很可能扩大 的取值范围,另外数形结合不会利用双曲线渐近线. 变式与引申 1:求函数的值域. 题型二 数形结合在不等式中的应用 例 2.若不等式的解集为区间,且,用心 爱心 专心1xyol3l2l1图 8-2则 . 点拨:通过数形结合的思想把一个解不等式的问题转化为求一条直线与半圆何时有交点. 解:令, .其示意图如图 8-3:若, 要 满 足, 则, 此 时. 从 而.若,要满足,则.则,从而 不存在. 易错点:如不能联想到直线与圆的图象,则思维很容易受阻.变式与引申 2:已知函数有两个零点,则有( )A. B. C. D. 题型三 数形结合在平面向量中的应用 例 3.在中,,G 为外心,求的值.点拨:结合图形,利用平面...