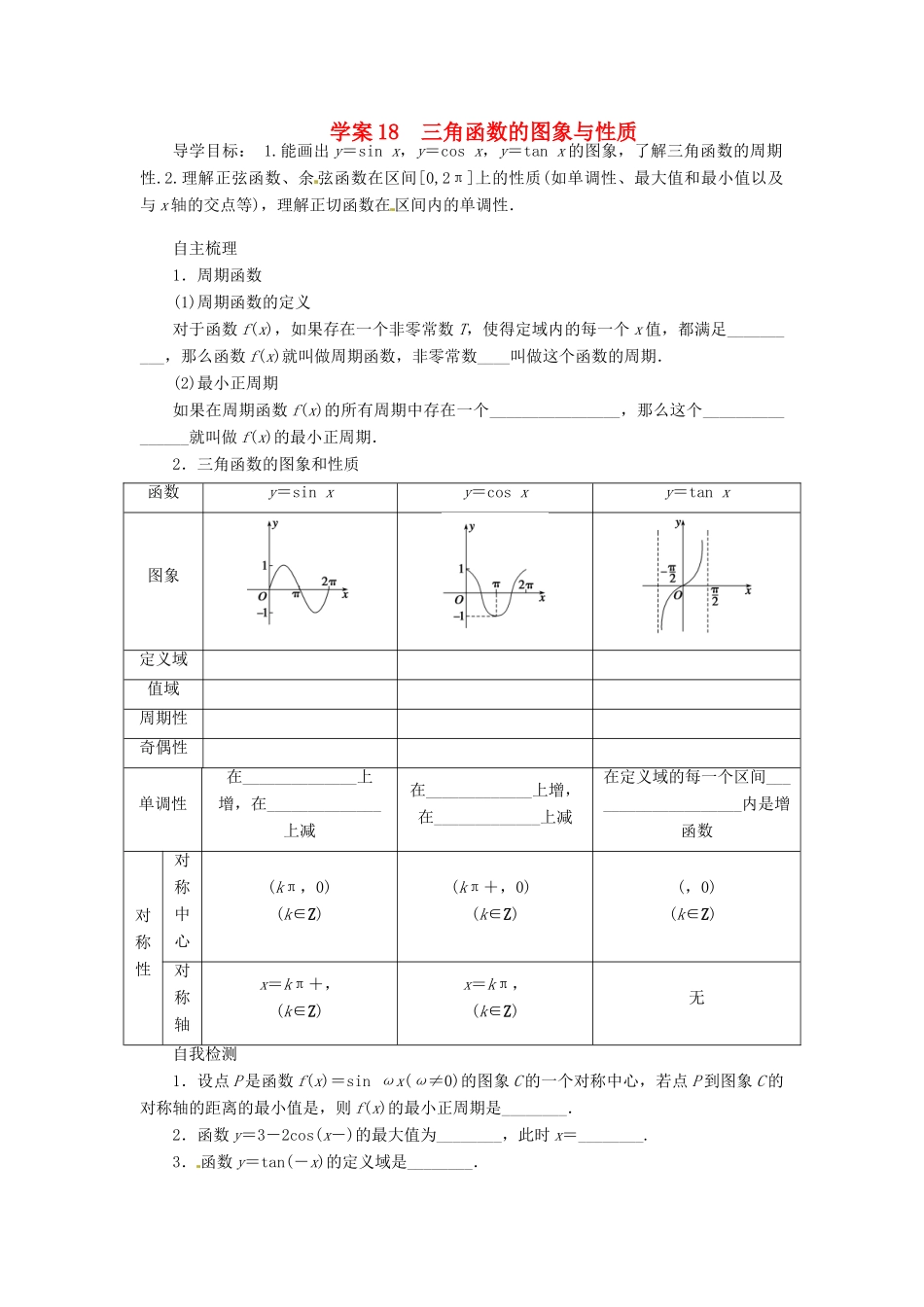
学案 18 三角函数的图象与性质导学目标: 1.能画出 y=sin x,y=cos x,y=tan x 的图象,了解三角函数的周期性.2.理解正弦函数、余 弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与 x 轴的交点等),理解正切函数在 区间内的单调性.自主梳理1.周期函数(1)周期函数的定义对于函数 f(x),如果存在一个非零常数 T,使得定域内的每一个 x 值,都满足__________,那么函数 f(x)就叫做周期函数,非零常数____叫做这个函数的周期.(2)最小正周期如果在周期函数 f(x)的所有周期中存在一个________________,那么这个________________就叫做 f(x)的最小正周期.2.三角函数的图象和性质函数y=sin xy=cos xy=tan x图象定义域值域周期性奇偶性单调性在______________上增,在______________上减在_____________上增,在_____________上减在定义域的每一个区间____________________内是增函数对称性对称中心(kπ,0)(k∈Z)(kπ+,0)[(k∈Z)(,0)(k∈Z)[对称轴x=kπ+,(k∈Z)x=kπ,(k∈Z)无自我检测1.设点 P 是函数 f(x)=sin ωx(ω≠0)的图象 C 的一个对称中心,若点 P 到图象 C 的对称轴的距离的最小值是,则 f(x)的最小正周期是________.2.函数 y=3-2cos(x-)的最大值为________,此时 x=________.3. 函数 y=tan(-x)的定义域是________.4.比较大小:sin(-)________sin(-).5.如果函数 y=3cos(2x+φ)的图象关于点中心对称,那么|φ|的最小值为________.探究点一 求三角函数的定义域例 1 求函数 y=+的定义域.变式迁移 1 函数 y=+lg(2sin x-1)的定义域为________________________.探究点二 三角函数的单调性例 2 求函数 y=2sin 的单调区间.变式迁移 2 (1)求函数 y=sin,x∈[-π,π]的单调递减区间;(2)求函数 y=3tan 的周期及单调区间.探究点三 三角函数的值域与最值例 3 已知函数 f(x)=2asin(2x-)+b 的定义域为[0,],函数的最大值为 1,最小值为-5,求 a 和 b 的值.变式迁移 3 设函数 f(x)=acos x+b 的最大值是 1,最小值是-3,试确定 g(x)=bsin(ax+)的周期.转化与化归思想例 (14 分)求下列函数的值域:(1)y=-2sin2x+2cos x+2;(2)y=3cos x-sin x,x∈[ 0,];(3)y=sin x+cos x+sin xcos x.【答题模板】解 (1)y=-2sin2x+2cos x+2=2cos2x+2cos x=2(cos x+)2-,cos x∈[-1,1]...