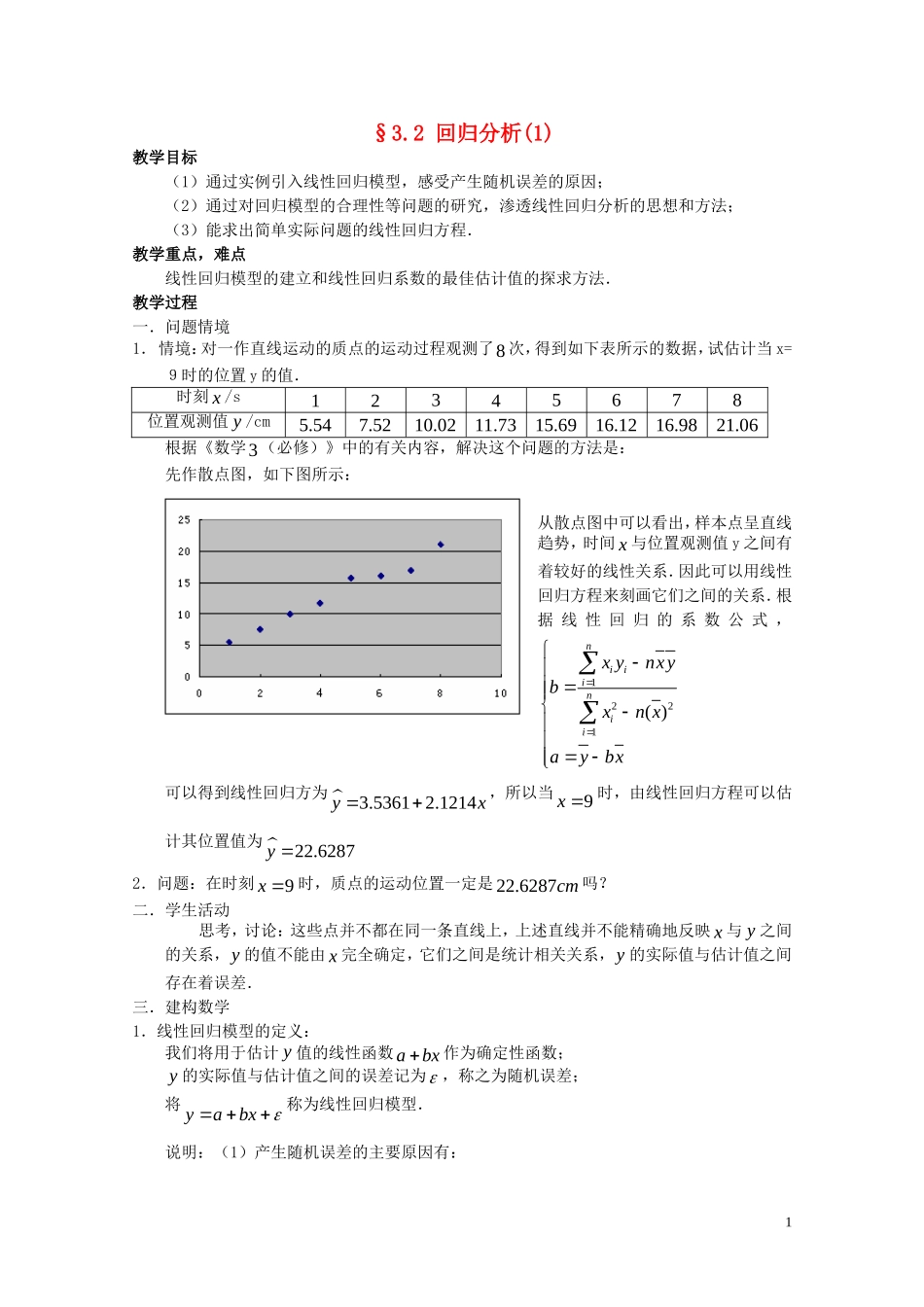
§3.2 回归分析(1)教学目标(1)通过实例引入线性回归模型,感受产生随机误差的原因;(2)通过对回归模型的合理性等问题的研究,渗透线性回归分析的思想和方法;(3)能求出简单实际问题的线性回归方程.教学重点,难点线性回归模型的建立和线性回归系数的最佳估计值的探求方法.教学过程一.问题情境1. 情境:对一作直线运动的质点的运动过程观测了8 次,得到如下表所示的数据,试估计当 x=9时的位置 y 的值.时刻 x /s12345678位置观测值 y /cm5.547.5210.0211.7315.6916.1216.9821.06根据《数学3 (必修)》中的有关内容,解决这个问题的方法是:先作散点图,如下图所示:从散点图中可以看出,样本点呈直线趋势,时间 x 与位置观测值 y 之间有着较好的线性关系.因此可以用线性回归方程来刻画它们之间的关系.根据 线 性 回 归 的 系 数 公 式 ,1221( )niiiniix ynxybxn xaybx 可以得到线性回归方为 3.53612.1214yx,所以当9x 时,由线性回归方程可以估计其位置值为 22.6287y 2.问题:在时刻9x 时,质点的运动位置一定是22.6287cm 吗?二.学生活动思考,讨论:这些点并不都在同一条直线上,上述直线并不能精确地反映 x 与 y 之间的关系,y 的值不能由 x 完全确定,它们之间是统计相关关系,y 的实际值与估计值之间存在着误差.三.建构数学1.线性回归模型的定义:我们将用于估计 y 值的线性函数abx作为确定性函数;y 的实际值与估计值之间的误差记为 ,称之为随机误差;将 yabx 称为线性回归模型.说明:(1)产生随机误差的主要原因有:1① 所用的确定性函数不恰当引起的误差;② 忽略了某些因素的影响;③ 存在观测误差. (2)对于线性回归模型,我们应该考虑下面两个问题: ① 模型是否合理(这个问题在下一节课解决); ② 在模型合理的情况下,如何估计a ,b ?2.探求线性回归系数的最佳估计值:对于问题②,设有n 对观测数据( ,)iix y(1,2,3,, )in,根据线性回归模型,对于每一个ix ,对应的随机误差项()iiiyabx ,我们希望总误差越小越好,即要使21nii越小越好.所以,只要求出使21( ,)()niiiQyx 取得最小值时的 , 值作为a ,b 的估计值,记为 a,b .注:这里的i就是拟合直线上的点,iix abx到点,iiiP x y的距离...